Методические рекомендации Методические рекомендации по расчету температурных полей, напряжений и деформаций в цементобетонных покрытиях

МИНИСТЕРСТВО ТРАНСПОРТНОГ О СТРОИТЕЛЬСТВА

ГОСУДАРСТВЕННЫЙ ВСЕСОЮЗНЫЙ ДОРОЖНЫЙ
НАУЧНО ИССЛЕДОВАТЕЛЬСКИЙ ИНСТ ИТ УТ
( С ОЮЗДОРНИИ )

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО РАСЧЕТУ ТЕМПЕРАТУРНЫХ ПОЛЕ Й ,
НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ В
ЦЕМЕНТОБЕТОНН Ы Х ПОКРЫТИЯХ

Моск в а 197 6

Одобре н ы Минтрансстроем

Изложены основные закономерности теп л оперед ачи в дорожных цемен т обетонны х покрытиях с учетом радиационного баланса и конвективного теплообмена , п риведены формулы и примеры расчета по ним температурн ы х полей , напряжений и деформаций в покрытиях .

Для практического использования подробно изложена методика применения гармонического анализа , позволяющего выразить аналитически л юбую функ ц ию распределения температуры по толщине покрытия во времени . Учитывая пожелания проектных и строительн ых организаций , все формулы даны в доступной для практического применения форме .

Предисловие

Измен е ния суточного хода температуры воздуха , интенсивности солнечной радиа ц ии , конвективного и кондуктивн о го теплообмена вызывают на поверхности и по толщине дорожных покрытий температурные напряжения , велич ин а которых в ряде случаев может достигат ь прочности бетона . Поэтому является обязательным учет как температурных напряжений и д еформаций при расчете тре щи ностойкости покрытий и работы швов , так и температуры тверден ия бетона при разработке технологии строительства покрытий .

В « Методических рекоменда ц иях по расчету температурных полей , напряжений и деформа ц ий в цементобетонн ы х покрытиях » обоб щ ены отдельные результаты экспериментальн ы х и аналитических исследований , проведенных в Союздорнии ( В . А . Черн иг овы м , Н . И . Мусорин ы м , О . Б . Федотовой , В . А . Лапшиным , Е . И . Броницким , В . А . Зел ь мановичем , Б . Б . Самойленко , Г . С . Бабаяном ), в други х институ тах ( Л . И . Горецким , И . А . М едниковы м , Б . С . Раев ы м - Богословским , Е . А . Палат ник овы м , А . В . Павловым , Э . Д . Б ондаревой , В . Д . Садов ы м , В . А . Воейковым ) и за рубежом . Настоящие « Методические рекомендации » предназначены для исполь з ования проектными и строительными организациями на стадии как проектирования , так и строительства бетонных покрытий .

« Методические рекомендации » разработал канд . т ехн . н аук В . А . Чернигов .

Замечания и предложения просьба направлять по адресу : 143900 Балашиха -6 Московской обл . , С оюздорнии .

Общие положения

1 . Температурный фактор определенным образом вли яет на формирование физических свойств бетона и на напряженно - д еформированное состояни е дорожной одежды в период эксплуатации дороги . При известных функциях изменения температуры поверхности и по толщине ц ементобетонного покрытия можно рассчитать :

величину и повторяемость температурных напряж е ний в плитах разной длины ;

продольную устойчивость покрытия ;

температурные деформации плит и швов ;

глубину промерзания и оттаивания грунта под дорожной одеждой .

2 . Самостоятельное значение имеет теплотехническое обоснование технологических процессов , обеспечивающи х :

тре щ иностойкость покрытия до нарезки поперечн ы х швов в затвердевшем бетоне ;

заданную скорость набора прочности бетоном ;

требуемую температуру твердения бетона по у с ловиям стойкости поверхностного слоя покрытия и формирования его оптимальной структуры ;

выбор требуемого способа ухода за свежеуложенн ы м бетоном ;

бетонирование покрытий в зимних условиях ;

бетонирование покрытий в условиях сухого и жаркого климата .

Расчет температурных полей в цементобетонных покрытиях

Основные закономерности теплопередачи в покрытии

3 . Изменение температуры в поверхностном слое и по т о лщине покрытия происходит вследствие меняюще го ся в нем теплосодержания , обусловленного процессами ра д иационной , конвективной и кондуктивной теплопередач . Направление тепловых потоков , составляю щ их тепловой баланс на поверхности покрытия , схематически показано на рис . 1 .

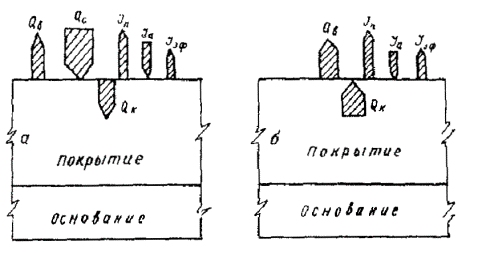
Рис . 1 . Схема составляю щ их теплового баланса на поверхности покрытия днем ( а ) и ночью ( б ):

Q с - коротковол н овая суммарная радиация (прямая и рассеянная); Q в - конвективная теплопередача; Q к - к ондук тивная теплопередача; J п - длинноволновое и з лучение покрытия; J а - д линноволновое из лучение атмосферы ; J эф = J п - J a - эффективное излу чение покрытия

4 . Радиационная теплопередача R в ы ражается радиационн ы м балансом и является мерой притока лучистой энергии к поверхности покрытия :

R = (Q п + Q р )(1 - A) - J эф ,                                                     ( 1 )

где Q п , Q р - потоки тепла соответственно от прямой и рассеянной радиации ;

A - велич и на , характеризующая отражение тепла в зависимости от цвета поверхност и , называемая коэффициентом альбедо поверхности .

5 . Конвективная теплопередача Q в между поверхностью покрытия и воздухом выражается законом Ньютона :

Q в = αк ( T п - T в ),                                                                   ( 2 )

где T п , T в - температура соответ с твенно поверхности покрытия и воздуха * ) ;

αк - коэффициент конвективной теплопередачи , зависящий от скорости ветра и перепада температуры Δ T = T п - T в .

*) Здесь и далее температура принята в °С.

6 . К он дук тивная теплопередача от поверхности к подошве или от подошвы к поверхности покрытия опре д еляется ( в данном случае ) приближенно законом Фурье :

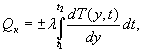                                                         ( 3)

где T ( y , t ) - ф ункция распределения температуры по т олщин е покрытия во времени ;

λ - коэффициент теплопроводности бетона .

7 . С учетом направления тепловых потоков R , Q в и Q к ( см . р ис . 1 ) уравнения тепловых балансов на п оверхности покрытия имеют вид :

днем : R = Q в + Q к или Q в = R - Q к ;                                              ( 4 )

ночью : Q к = Q в + J эф или Q в = Q к - J эф .                                          ( 5 )

В уравнениях ( 4) и ( 5) не учтены затраты тепла на испарение влаги с поверхности покр ы тия , так как при сухой погоде эти затраты ничтожны .

8 . Подставив в уравнения ( 4 ) и ( 5 ) значения Q в = α( T п - T в ), найдем температуру поверхности п о крытия T п и коэффициент конвективной теплопер ед ачи α :

днем :   и                                      ( 6)

ночью :   и                                 ( 7)

Формулы ( 6) и ( 7) дают ясное представление о влиянии каждой составляющей теплового баланса на температур у поверхности покрытия и будут далее использованы в расчетах .

9 . Численные значения параметров радиационн ог о баланса приведены в справочниках по климату или м огут быть получены на метеорологических стан ц иях , р асположенных в районе строительства дороги . В С Н иП II - А .6 -72 приведены данные по радиации з а июль и суточный хо д освещенности горизонтальной поверхности по месяцам .

Известно , что суточный ход температуры воз д уха является периодическим и приближается к прост ом у гармоническому , например синусои д альному , виду с периодом 24 ч . Гармонической функцией , но более сло ж ного вида , является такж е суточный ход радиационного баланса .

В зависимости от месяца длительность и величи на прямой и рассеянной солнечной ра д иации в дневные ч а сы суток ра з лична . По этой причине происходит периодическое изменение температуры поверхности покрытия в течение любых суток года , которо е в сегда можно строго описать тригонометрическим рядом .

10 . Тепловые потоки в эксплуатируемом покрытии практически всегда направлены перпендикулярно к поверхност и покрытия . И только до устройства обочин , вблизи оголенных торцов покрытия , наблюдается дву х мерное температурное поле .

11 . Закономерности изменения температуры по тол щ ине покрытия дороги можно описать качественно следующими известными тремя законами Фурье о распространении температурных волн в полупространстве :

амплитуда колебаний экспоненциально убывает с глубиной ;

температурные колебания в покрытии происходят со сдвигом фазы , т . е . максимумы ( минимумы ) температуры , например , на подошве запаз д ывают по сравнени ю с максимумами ( минимумами ) температуры на поверхност и ;

глубина проникания температурной волны возрастает с увеличением перио д а колебаний температуры на поверхности покрытия .

1 2 . При толщине покрытия 20 см в натурных у с лови ях наблюдается отставание максимальной температуры на подошве покрытия в среднем на 4 - 5 ч по сравнению с максимальной температурой на поверхности .

13 . При ясном небе ( облачность 0 - 2 бал л а ) ма к симальн ая температура поверхности покрыти я наблю д ается к 14 - 15 часам , а минимальная - в 4 - 6 часов, что соответствует наибольшей и наименьшей температуре воздуха в эти часы . В это время изменение температуры по тол щ ине покрытия приближается к линейному в иду .

14 . В ясные зим н ие ночи температура повер хн ости покрытия може т быть ниже т емпературы воздуха , что следует из формулы ( 7 ) , при J эф > Q к . Это явление наиболее вероятно для Средней Азии , Казахстана и Восточной Сибири .

15 . Ле т ом температур а поверхности покрытия ночью , как правило , выше температуры в оздуха на 2 - 6 ° С и зависит о т скорости ветра и облачности .

16 . Через 2-3 ч после восхода солнца возникает почти безградиентное распределение температуры по толщине покрытия (12 - 24 см ).

17 . В перио д захода солнца температур а поверхност и близка к среднесуточной температуре по в ерхности и выравнивания температуры по толщи н е покрытия не наблюдается . С этого времени температура поверхности становится ниже температуры подошвы , и через 1 - 2 ч после захода солнца тепловые потоки полностью направлены к поверхности покрытия .

18 . При установившихся суточных перио д ических колебаниях температуры поверхности покрытия колебания ее суточных амплитуд по толщине практическ и происходят относительно оси среднемесячных распре д елен ий температуры ( в расчетном месяце ) с периодом , ра вным году ( р ис . 2 , а ) . М аксимальная и минимал ь ная среднемес я чные температуры поверхности наблюдаются в к онц е июля и января .

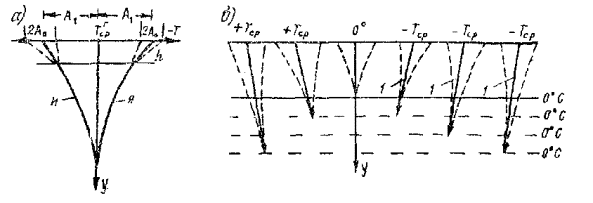
Рис . 2 . Схема колебаний суточных амплиту д A температуры по глубине y , относительно оси сре д немесячной температуры в январе (Я), июле ( И ) и в первый меся ц от начала промерзания относ и тельно оси 1

1 9 . В тех случаях , ког д а после ясных д ней устана в лив аетс я пасмурная погода или происходит п охолодание , среднемесячное распределение температуры по тол щ ине до 2 - 3 м сильно искажается и не являетс я осью , относительно которой происходят суточные колебания амплитуд температуры . В этих случаях при известном распределении температуры на поверхности покр ы тия для решения задачи распределения температуры и направления тепловых потоков по тол щ ине покры ти я может быть использован гармонический анализ .

20 . В п ервый месяц от начала промерзания или оттаивания грунта основания и земляного полотна ( примерно до 40 - 50 см ) суточные амплитуды температ уры колеблются относительно средней температуры по тол щи не покрытия , выражаемой линейным уравнен ие м ( рис . 2 , б) :

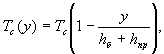                                                   ( 8)

где T c - среднесуточная температура на поверхности покрытия ;

h б - толщина покрытия ;

h пр - глубина промерзания - оттаивания гру н та под подо ш вой покрытия ;

y - ордината с отсчетом от поверхности покрытия .

2 1 . Изложенные закономерности теплопередачи в бетонных покрытиях являются общими для любых климатических условий , влияние которых проявляется через величины и повторяемость суточных амплитуд температуры на поверхности покрытия в зависимости от суточных амплитуд температуры воздуха , интенсивности и длительности в течение дня солнечной радиации и числа ясных , полуясных и пасмурных дней в году .

Расчет температуры поверхности покрытия

22 . Решение теплотехнических задач возможно при известных граничных и начальных условиях . Граничное условие задается функ ц ией изменения температуры на поверхности покрытия и на определенной глубине , а начально е условие - функцией распределения температуры по тол щ ине в нача л ьное время .

23 . Максимальная и минимальная температура поверхности покрытия в течение суток может стать в ряде задач граничным условием или оказаться вспомогательной предельной величиной температуры при за д ании граничного условия , например , гармонической функцией . При отсутствии кондуктивной теплопередачи в покрытии ( после 2 - 3 ч от восхода солнца , см . п . 16 ) температура на поверхности покрытия может быть принята за начальное условие в задачах , например , распр е деления температуры по толщине .

24 . Максимальную температуру пов е рхности покр ы тия T п max днем , соответствующую максимальной температуре воздуха T в , найдем по ф о рмуле ( 6 ):

                                   ( 9)

Тепловой поток Q к от поверхности покр ыти я толщиной h приближается в это время к стаци он арному и согласно форму л е ( 3) выражается как

Q к = 5λ · град T 1 h ,                                                         ( 10)

где град T 1 - максима л ьный градиент температуры в покрытии , равный 6 0 ° С / м в умеренном и 85 °С / м в континентальном климате ;

λ - коэффициент теплопроводности бетона .

25 . Минимальную температуру поверхности покры ти я T п min ночью , соответствующую минимальной температуре воздуха T в , найдем по формуле ( 7 ):

                                                   ( 11)

2 6 . Тепловой поток Q к к пов е рхности покрыти я в формуле ( 11 ) приближается в это врем я к ста ц ионарному и равен

Q к = 5 · λ · град T 2 · h ,                                                   ( 12)

где град T 2 - максимальный градиент температуры в покрытии, р авны й 40 °С / м в умеренном и 57 °С / м в континентальном климате .

27 . При безградиентном температурном поле в покрытии , наблюдаемом после 2 - 3 ч о т восхода солнца , температуру поверхности T п и по толщине T ( y ) определим по формуле ( 6 ), приняв Q к = 0:

                                    ( 13)

28 . Для практических расчетов суточное изменение температур ы T (0, t ) поверхности покрытия с пери о дом T 0 , равным , например , 24 ч , выразим простой гармонической функцией :

                        ( 14)

где   Tc = T п (max) - A0;  

В данном случае начальная фа з а   выражает расчетное отклонение температуры в долях периода T 0 от положения равновесия - средней температуры T c .

29 . Изменение суточной температуры поверхнос ти T (0, t ) покрытия с учето м колебаний температуры в годовом цикле ( см . п . 18 ) найдем как сумму суточны х и годовых колебаний :

T (0,t) = T1 + A1sin ω 1 t 1 + A0sin( ω t - φ 0 );                                     ( 15)

 

где T 1 - среднегодовая температу ра поверхности п окр ы тия ;

A 1 - среднегодовая амплитуда колебаний температуры на поверхности покрыти я ;

T п( max , июль ) - максимальная температура поверхност и покрытия в июле , определя е мая по формуле ( 9 );

T п( min , январь ) - минима л ьная температура повер х ности покрытия в январе , опре д еляемая по формуле ( 11 );

A 0 (июль) , A 0 ( январь ) - максимальные суточные амплитуды колебаний температуры на поверхности покрытия соответственно в июле и январе , определяемые по формуле ( 14);

T 12 - период колебаний годовой темп е ратуры , равный 12 меся ц ам ;

t 1 - число месяцев , назначаемое от 1 до 12 .

30 . Расчет по формулам ( 9 ) - ( 15 ) приведен в приложении 1 , а описание температуры поверхности тригонометрическим рядом - в приложении 2 .

Расчет распределения температуры по толщине покрытия

3 1 . При стационарном кондуктивном теплообмене в покрытии распре д еление температуры T ( y , t ) по толщине выраж а ется линейными функциями :

 при T 1 = T п - T пд и T п > T пд ;                                         ( 16)

 при T 2 = T пд - T п и T п < T пд ;                                                 ( 17)

 при T п > T пд ;                                                    ( 18)

 при T п < T пд ,                                                    ( 19)

г д е T пд - температура на подошве покрытия .

При этом в срединной плоскости плиты температ у ра , заданная функц и ями ( 16), ( 17) и ( 18 - 19), соответственно равна :

   

32 . Изменение температуры T ( y , t ) в любые часы суток по тол щ ине покрытия при граничном условии на поверхности в виде гармонической функции может быть приближенно найдено на основе известного решения о распространении температурных волн в полупространстве :

 0 ≤ y < ∞ , Ty = 0 = A0cosωt,

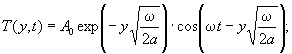                                ( 20)

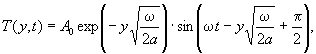
где a - коэффициент температуропроводности бетона , м2 / ч .

В формуле ( 20) экспонента 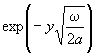  дает коэффициент снижения амплитуды Aa по толщине покрытия , а  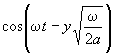- изменение амплитуды во времени со сдвигом фазы на величину   ( см . п . 11).

33 . Используя формулу ( 20 ) и начальное условие о нулевом градиенте в покрытии после 2 - 3 ч от восхода солнца , получим расчетную формулу :

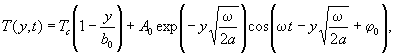                       ( 21)

где φ 0 - сдвиг фа з ы температуры поверхности покрытия от T п max до T нач при t = 0,

  выражаемый в градусах или радианах ( например , при T п max в 14 часов , T нач в 7 часов и T o = 2 4 ч будем иметь  или φ 0 = 90 + 15 = 1 05 ° с отсчетом времени t = 0 в 7 часов ).

Величину коэффициента b 0 в формуле ( 21 ) найдем и з равенства T (0,0 ) = T ( y ,0 ) или

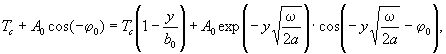
откуда 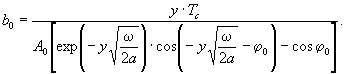                                              ( 22)

При наличии экспериментальных данных о суточном ходе температуры поверхности покрытия или расчетных данных о температуре поверхности через 2 - 3 ч после восхода , в 1 3 - 1 4 часов и во время захода солнца расче т распределения температур по толщине можно произвести приближенно на основ е гармоническ о го анал и за путем подбора постоянных коэффи ц иентов в ряде Фурье ( см . п риложение 2).

Расчет температурных напряжений в бетонных покрытиях

Расчетные формулы термонапряженного состояния покрытия

34 . Температурные напряжения всегда возникают в покрытии при несостоявшихся температурны х деформац и ях - про д ольных и коробления ( изгиба ). Поэтому , тем п ературн ые напряжения в покрытии нельзя измерять датчиками деформаций ; их можно определить расчетом , например на основе известной формулы С . П . Т имош енк о, которая для цилиндрического изгиба плиты ( края покрытия ) и меет вид :

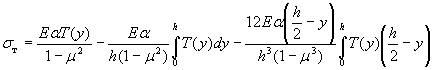              ( 23)

г д е σ т - температурное напряжение в п окрытии ;

α - коэффициент линейного температурн о го расширения бетона ;

E - мо д уль упругост и бетона ;

μ - коэффи ц иент Пуассона , для бет о на равн ый 0 , 15 - 0,20, ч то д ае т (1 - μ 2 ) ≈ 1 ;

T ( y ) - расчетная функция распределения т е мпературы по толщине покрытия .

В правой части формулы ( 23) первый член выража е т напряжения σ 1т , во з никающие в покрытии при невозможности д еформаций продольных и коробления ; второй член - σ2т при невозможности только продо л ьных деформаций ; третий - σ3т при невозможности только деформаций коробления . Следовательно , для свободного края покрытия без поперечных швов получ и м

σ1т = E αT ( y ).                                                                ( 24)

Для свободного края середины плиты , которая под действием собственного веса не может коробиться и гд е беспрепятственно возникает продольная температурная д еформация , по л учим

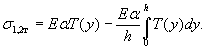                                            ( 25)

35 . Если бы плита была невесомой и могла полностью коробиться и продольно смещаться , то при н е линейном распределении температуры по толщине в ней возникли бы напряжения , которые принято называть собственными напряжениями , опреде л яемые по формуле ( 23 ). В этом случае напряжения σ1,2т найденн ы е по формуле ( 25 ), оз н ачают сумму напряжений от н е возможности коробления ( изгиба ) плиты и собственных напряжений , т . е ., иначе , разность первых д вух членов (σ1т - σ2т ) не равна третьему члену σ3т в форм ул е ( 23 ) или

σ1,2т = σ1т - σ2т = σт + σ3т                                                         ( 26 )

Если возможно частичное коробление п литы , т о напряжения уменьшаются пропор ц ионально коэффициенту Cx , определяемому по известному графику Бредбери . В этом случае формула ( 26) примет вид :

σ1,2т = σ т + σ3т · Cx = σ1т - σ2т - σ 3т + σ3т · Cx = σ1т - σ2т - σ 3т (1 - Cx ).                     ( 27 )

При Cx = 1, что означает невозможность коробления плиты , получим формулу ( 26) или соответствующую ей ( 25). Вывод формулы ( 27) справедлив при наличии напряжений растяжения при изгибе на подошве плит ы , обусловленных третьим членом в формуле ( 23).

36 . С понижением или повышение м температуры плита соответственн о сокращается или удлиняется . При этом на ее подошве возникают силы трения - сцеплен и я , в результате которых в плите появляются осевые напряжения σ р растяжения или сжатия , определяемые на основ е известной формулы Кулона N = hQ , или

N = σ р · h · b;                                                ( 28)

откуда

где h - коэффициент трения - сцепления между подошво й плиты и основанием ;

γ - плотность бетона ;

l - длина плиты между поперечными швами .

Более сложные формулы , по сравнению с выражением ( 28), учиты в ающие деф о рмации плиты и функцию температуры , представляют интере с в исследовательс к их целях . Для и нженерных расчето в вполне пригодна формула ( 28), так как напряжения при изменении коэффициента трения от 0,5 п о 1,5 сравнительно малы .

При современных конструкциях д орожных о деж д увеличение длины плиты на каждые 1 0 м приводит к незначительном у увеличению напряжений : на 1 - 2 к гс / см2 . Поэтому в коротких плитах длиной 4 - 8 м напряжения σр в большинстве случаев можно не учитывать .

Расчет температурных напряжений при линейном распреде л ении температуры по толщине покрытия

37 . При линейном распределении температуры в покрытии и невозможности продольных деформа ц ий и короблени я температурные напряжения по тол щ ине о п ределяют по формуле ( 24 ) с подстановкой соответствую щ ей функ ц ии T ( y ) из выражений ( 16 ) - ( 19 ). Из формулы ( 24 ) следует , что взаимовлияни е между напряжениями в различных плоскостях покрытия не возникает при повсюду одинаковой толщине покрытия и равных величинах E и α бетона по толщине и длине покрытия .

38 . Если плита не имеет во з можности короби ться ( Cx = 1) , а продольные деформа ц ии проявля ю тся по л ностью , то расчет температурных напряжений σ т производят по формуле ( 25 ) с учетом T ( y ) из ( 16 ) - ( 17 ), или

                                                ( 29)

                                                ( 30)

Из формул ( 29) - ( 30) видно , ч то по толщине пл и ты возникают только напряжения изгиба . Напряжения со знаком « плюс » соответствуют напряжениям сжатия при изгибе , со з наком « минус » - растяжения при изгибе . Продольные деформации и соответствующие и м напря ж ени я , в ыражаемые вторы м членом правой части формулы ( 25) , пропорциональны перепаду температуры в срединной плоскости плиты .

39 . При частичном короблении плиты выпуклостью вверх ( Cx < 1) температур н ые напряжения находят по формуле ( 27 ), что равносильно умножению правой ча с ти формулы ( 29 ) на коэффициент Cx < 1:

 при                                ( 31)

Расчет температурных напряжений при гармоническо м изменении температуры в покрытии

40 . При отсутствии в покрытии продольных деформаций и коробления температурные напряжения определя ют по формуле ( 24 ) с учетом гармонической функции температуры T ( y , t ) , выраженной , наприме р , формулой ( 21 ) . Чтобы определить напряжения σ 1т на подошве или поверхности покрытия по формуле ( 24 ), достаточно в формуле ( 21 ) принять соответственно y = h или y = 0.

4 1 . При свободных продольных деформациях расче т температурных напряжени й в плитах , не имеющих возмо ж ности коробиться ( Cx = 1) или имеющих частичную возмо ж ность коробления ( Cx < 1 ), производят по формуле ( 27 ), к о торую запишем в полном виде :

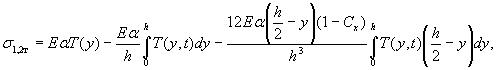  ( 32)

г д е T ( y , t ) - гармоническая функция темп ер атуры по т олщине пок ры тия , заданная , например , формулой ( 21).

Пр и Cx = 1 формула ( 32) соответствует формуле ( 25).

Для интегрирования фун к ции ( 21 ) в формуле ( 32) следует выразить cos ( α - β ) = cosαcosβ + sinαsinβ и далее произвести интегрирование сог л асно известным табличным интегралам :

Конечная расчетная формула σ 1,2т получае тся громоздкой и мало приемлемой для практики из -з а вероятных ошибок при вычислениях . Поэтому це л есообразно е в каждом конкретном случае построить по формуле ( 21) график распределени я температуры в плит е , найти значения интегралов по правилу трапе ц ий ( приложение 3) или Симпсона и произвести вычисления σ т по формулам ( 25) или ( 32).

Расчет температурных деформаций плит и поперечных швов в покрытии

42 . В общем случае продольные температурные деформации Δ l т или относите л ьные температурные деформации ε т плит равны :

Δ l т = α l ( T н - T к );                                                              ( 33)

                                                      ( 34)

где l - длина плиты ;

T н - начальная температура , соответствую щ ая расчетному началу охлаждения и ли нагре в а плиты ;

T к - конечная температура , соответству ющая расчетному кон ц у охлаждения или нагрева плиты .

43 . Для определения расчетных температур T н и T к воспользуемся вторым членом правой част и формулы ( 23 ):

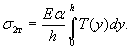                                                      ( 35)

Напряжения σ2т возникают в плите ( см . п . 34) при невозможности только продоль н ых деформа ц ий . Поэтому средняя температура в покрытии , которую можн о принять за расчетную начальную T н или конечную T к , будет равна

                                                          ( 36)

При линейном распределении температуры по толщине плиты расчетная температур а T c , как это следует из формулы ( 36), п ри   будет равна температуре в срединной плоскости, и л и  ( см . п . 31 ) .

При нелинейном распределении температуры по толщине покрытия средняя температура может значительно отличат ь ся от температуры в срединной плоскости , что объясняется изменением волны температуры в плите по экспонен ц иальной зависимости и отставанием во времени максимальной амплиту д ы ( см . п . 12). Находить среднюю температуру следует по формуле ( 36 ) .

44 . Продольную температурную деформацию Δl т плиты за любое время суток Δ t = t 1 - t 2 определяем по формуле ( 33 ), вычислив предварительно T н и T к по формуле ( 36 ):

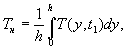
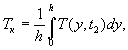                                      ( 37)

г д е T ( y , t 1 ), T ( y , t 2 ) - суточные функции температуры по толщине покрытия , выражаемые формулой ( 21) , в момен ты времени t 1 и t 2 .

Интегрирование функ ц ии ( 21 ) в формуле ( 37 ) с леду ет производ и ть приб л иженно по правилу тра п еций .

П родол ьны е деформации Δ l т плиты за мес я ц и ли год с достаточной точностью можно определ и ть , н айд я среднюю температуру в д анный момент време н и , равную температуре и срединно й плоскости плит ы при линейном перепаде по толщ ин е .

Для этого вычисляют температуру повер х ности п литы по формуле ( 15) и далее по формулам ( 16) и л и ( 17 ) находят расчетную температуру в сре д инной плоск о сти плиты , приняв гра д иенты температуры гра д T в за в исимости от климата по пп . 24 - 26.

45 . Ширина раскрытия поперечных швов между примыкающими плитами одинаковой д лины , к азалось бы, д олжна быть равна продольной деформа ц ии одной плиты и определяться п о формулам ( 33 ) - ( 37 ). Однако в натурных условиях геометрическая и физическая середины плит н е совпадают , что объясняется неравномерным распределением сил трения - сцепления по подошве плиты и сил от возможного смерзания подо ш вы или боковых граней плит с грунтом . Натурные измерений деформаций 10 - 12 последовательно расположенных ш вов дают обычно деформации отдельных швов , различающиеся в 1 ,3 - 1,5 раза . Сумма деформа ц ий всех 10 - 1 2 швов обычно равна расчетной величине , а распре д еление деформа ц ий соответствует зако н у Гаусса . Учитывая это об с тояте льство , с ледуе т полученную по формуле ( 33 ) ширину раскрытия паза поперечного шва принимать з а среднюю в еличину при средне кв адратическом от к лонении σ = 0,15 Δl т . Следов а тельно , максимальная и минимальна я расчетные д еформации паза шва будут равны :

Δl = αl ( T н - T к )(1 ± 0,45) .

Нар я ду с температурными деформа ц иями в первы е 1 ,5 - 2 год а наблюда е тся усадка бетона плит , к оторая эквивалентна деформациям от понижения температуры на 10 - 1 2 ° С . При рез и нобитумны х мастиках , которыми периодически ( через 2 - 3 го да ) заполняют швы , едва ли ц елесообразно учитывать в расчетах деформации паза от усадок бетона , так как усадка бето н а приводит к увеличению ш ирины п аза. Если приме н ять герметики работающие в пазе бо л ее 4 л ет, то при расчете деформации паза следует увеличивать расчетный перепад температуры ( T н - T к ) на 1 0 ° С. Учет усадки бетона приве д ет к необходимости нарезки пазо в шв а большей ш ирины ( приложение 4).

В перио д эксплуата ц ии цемен т обетонных покрытий на уклона х д орог раскрытие швов между плитами меньше , чем на гори з он тальных участках . Это явление обусловлено не к оторым сползанием плит по н ап равле ни ю уклона покрытия . Поэтому на таких участках дорог и д л я оценки предель н ой растяжимости масти к - герме тик ов нет на д обности производить расчет раскрыти я ш вов в летне - осенний период до начала промерзания основания .

46 . У всех видов маст ик - герме тик ов , применяемы х в настоя щ ее время для заполнения пазов швов , с понижением температуры резко снижаются вязкие и деформати вны е свойства. В зависимости от климатичес ки х условий расчетная минимальная температура , соответствующая предельной величине раскрытия ш ва , может изменяться от минус 5 ° С в южных района х СССР до ми н ус 50 ° С и ниже в северных районах . Сама же мас тика , нахо д ясь в пазе , будет иметь минимальную температуру зимой , практическ и равную температуре поверхности покрытия . Поэтому изложенны е расчеты температурных поле й и д еформаций швов указывают на необходимость дифферен ц ированного назначения ш и рины п аза ш ва не только в зависимости от д лины пли т предельной продольной деформа ц ии , но и в зависимости от предельной растяжимости мастик в расчетном диапа з оне температур заданного кл и матического района . Это означает , что при одинаковых свойствах мастик и и геометрических размерах плит ширина паза шва в южных районах должна быть мен ь ше , чем в северных .

ПРИЛОЖЕНИЯ

Приложение 1

Примеры расчета температуры покрытия

При ме р 1 . Найти температуру поверхности покрытия в Московской обл . в 14 часов ию л я .

Дано : Tb = 25 ° С ; облачность 0 - 2 балла ; Q п + Q р = 559 + 1 05 = 6 64 ; J эф = 72 ; A = 0,3; град T = 0,6 ° С / см = 60 ° С / м ; h = 20 см ; α = 20 ; λ = 2 .

По формуле ( 10) найдем Q к = 5 · 2 · 60 · 0,2 = 1 20 к к ал .

По формуле ( 9 ) получим искомую температуру п о ве рхн ости

Пр име р 2 . Найти температуру поверхности покрытия в Московской обл . в 7 часов июля .

Дано : Tb = 14 ° С ; облачность 0 - 2 балла ; Q п + Q р = 270; J эф = 72; град T = 0; Q к = 0; A = 0, 3; α к = 20.

По формуле ( 13) найдем  °С.

Пр име р 3 . Найти минимальную температуру по в ерхности покрытия в Московской обл . в 4 часа июля .

Дано : Tb = 10 °С ; J эф = 70; λ = 2; Q п + Q р = 0; гра д T = 40 ° С / м ; h = 20 см ; α к = 3 .

По формуле ( 12 ) имеем Q к = 5 · 2 · 4 0 · 0,2 = 80 ккал .

По формуле ( 11) получим

Пр име р 4 . Найти максимальную температуру поверхности п окрытия в Московской обл . в 14 часов июля с учетом колебаний температуры в годовом цикле .

Дано: T п( max ,июль) = 38,6 ; T п( min ,июль) = 13,3, T п( min ,январь) = -30 °С .

Опре д елим по формулам ( 14) и ( 15) величины А0 , A 1 , T 1 :

A 0 = (38,6 - 13 ,3 ) : 2 = 1 2,6 5 ° С ;

При t 1 = 3 месяцам , φ 0 = 0 и t = 6 ч по формуле ( 15) най д ем

Расчет T (0 , t ) по формуле ( 15) дает лучшее прибли ж ение к результатам натурных измерений T (0, t ) в дневные часы и худшее - в утренние , что объясняется отклонением в утренние часы хода температуры от синусоиды .

Пр име р 5 . Найти температуру подошвы покрытия в Московской обл . в 14 и 19 часов июля .

Дано : T ср = 26 °С ( см . пример 1 и 2); A 0 = 12 ,65 °С; a = 0,003 ; h = 20 см ; φ 0 = 15 ° C .

Найдем параметр b 0 по формуле ( 22 ):

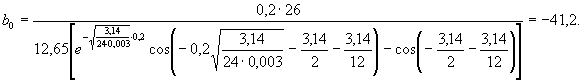
Температур у подошвы покрытия в 14 и 19 часов оп ределим по форм ул e ( 21 ):

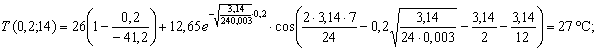
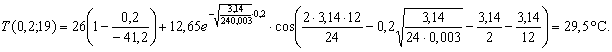
Максимальная температура подошвы покрытия 29 ,5 ° C ( так как cos 0 = 1) наблюдается в 1 9 часов , а макс и мальная температура поверхности - в 1 4 часов .

Приложение 2

Примене н ие практического гармонического анализа при расчете температуры покрытия

Суточный ход температуры поверхности покрытия отличается о т периодической функ ц ии , выражаемой , например , простой синусоидой . Если сложить отдельн ы е синусоиды с частотами и периодами , кратными наименьшей и з них , то получится периодическа я фун кц ия более сложного вида :

                                          ( 1)

Разложение каждого члена ряда ( 1) по формуле для синуса суммы приводит к ряду Фурье :

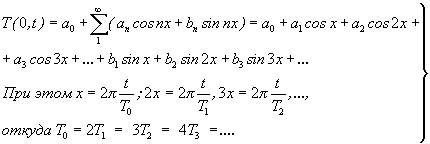              ( 2)

Для первых пяти гармоник к оэффициенты a 0 , a 1 , a 2 , a 3 , a 4 , a 5 , a 6 , b 1 , b 2 , b 3 , b 4 , b 5 находят п о следующим формулам :

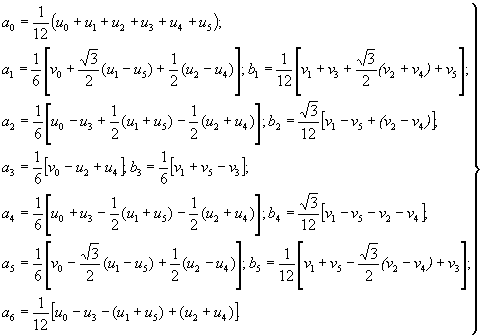               ( 3)

Вычисление в еличин u и v , в ход ящ их в формулы ( 3), произво д ят , пользуясь таб л . 1 д ля двенад цати ординат :

Таблица 1

y 0

y 1

y 2

y 3

y 4

y 5

y 6

y 11

y 10

y 9

y 8

y 7

Суммы ( u )

u 0

u 1

u 2

u 3

u 4

u 5

Разно ст и ( v )

v 0

v 1

v 2

v 3

v 4

v 5

Пример 1 . В результате натурных замеров через каждые два часа в течени е суто к полу ч ены вел ич ины температуры поверхности покрытия , указанные в таб л. 2 ( крайние значения температуры н а расстоянии одного периода должны находиться в одинаковых фазах ).

Таблица 2

Время суток , ч

7

9

11

1 3

15

17

19

21

23

1

3

5

7

Температура поверхности , °С

1 7

23

29

33

34

32

27

22

20

17

1 5

14

17

Ординаты y

y 0

y 1

y 2

y 3

y 4

y 5

y 6

y 7

y 8

y 9

y 10

y 11

y 0

Требуется выразить аналитически суточный ход температуры T (0, t ), т . е . опре д елить коэффициенты a 0 , a n , b n и число членов ряда ( 2), дающих в сумме достаточное приближение к измеренной температуре .

По табл . 1 найдем суммы u и разност и v :

17

23

29

33

34

32

27

14

18

17

20

22

Суммы ( u )

44

37

44

50

54

54

Разности ( v )

-10

9

14

1 6

14

10

По формуле ( 3) определим коэффициенты :

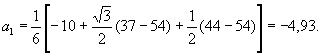
Аналогично получены a 2 = - 1,6; a3 = 0; a4 = 0; a5 = 0; a 6 = 0,08; b1 = 8,22; b2 = -0,146; b3 = 0,5; b4 = - 0, 146; b5 = 0,27.

Вычисления a n и b n проверим по формулам :

y 0 = a0 + a1 + a2 + a3 + a4 + a5 + a6 = 2 3,5 - 4,9 3 - 1,6 + 0 + 0 + 0 + 0,08 = 17,08;

Вычисления коэффи ц ие нтов прави л ьны , и ряд ( 2) примет в ид :

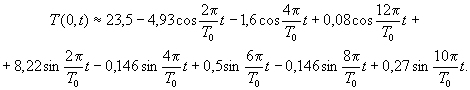
При T 0 = 24 ч и t = 0 получим T (0,0 ) = y 0 = 17 ° С в 7 часов . Ес л и T 0 = 24 ч , t = 6 ч и , т о T (0 ,6 ) = 33, 01 ° С в 1 3 часов . Таким образом , имее м практически равенство расчетной температуры с измеренной . Причем , от первых двух чле н ов ряда пол уч аем T (0,6 ) = 32,88 ° С .

Чтобы выразить T (0, t ) в виде ряда ( 1), необходимо найти амплитуды A n и начальные фазы φn каждой гармоники по формулам

 и                                                     ( 4)

В зависимости от знако в a n и b n , находят четверть , в которой лежит угол φn , по табл . 3 .

Таб л ица 3

a n

b n

φn

φn = f(αn)

+

+

I

φn = αn

+

-

II

φn = 180° - αn

-

-

III

φn = 180° + αn

-

+

IV

φn = 360° - αn

Тогда будем им е ть угол φ 1 в IV четверти , A 0 = a 0 и далее :

 

По числу -0,6 най д ем угол , равный 3 1 ° , и обоз н ачим его α1 = 31° . Согласно табл . 3 φ 1 = 3 6 0 - 31 = 329°. Аналогично находят A 2 , A 3 , ..., A n и φ 2 , φ 3 , ..., φn .

Таким образом, получим :

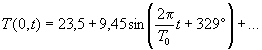
или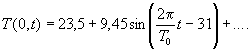

При известной функции температуры T (0 , t ) п о верхности покрытия , выраженной рядом Фурье , расчет температуры по толщине покрытия можно приближенно произвести на основе решения о распространения темпера т урны х волн в полупространстве . Применительно к бетонным покрытиям такое решение использовал в 1 938 г . К . Эберле в виде :

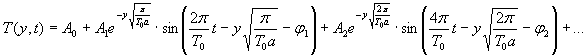( 5)

Формула ( 5) равно з начна формуле вида :

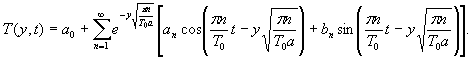               ( 6)

Используя третий закон Фурье и данные натур ных измерений ( через каждые 2 ч ) температуры в покр ы тии за сутки , К . Эберле решал две задачи расчета :

- коэффициента теплопроводности бетона по известной зависимости отношений амплитуд :

                                                ( 7)

где

- глубины проникновения суточных амплитуд по формул е ( 5).

Эберле пришел к выводу , что по ф ормулам ( 5) и ( 7 ) нельзя найти коэффициент теплопроводности бетона . Вычисленный таким образом коэффи ц иент λ почти в 2 раза больше измеренного . Данны е расчета затухания по глубине амплитуд температуры хорошо согласуются с натурн ы ми измерениями , и на г л убине 203 см от поверхности покрытия суточные амплитуды температуры практически равны нулю .

В 1 974 г . болгарский инженер Б . Волчев опубликовал следующую форму л у :

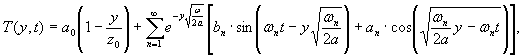
в которой задан нулевой градиент температуры при t = 0 . Способа определения параметра z 0 Б . Волчев не приводит , но обращает внимание на то , что результаты расчета T ( y , t ) по этой формуле почти совпадают с данными натурных измерений .

Приложение 3

Примеры расчета температурных напряжений в покрытии

Пример 1 . Найти температурные напряжения на поверхности и подошве плиты при невозможности коробления и линейном распределении температуры по толщине .

Дано : T 1 = 38 ,6 - 27 = 11,6 ° С ; E = 350000 к гс / см2 ; α = 10-51/ ° С ; h = 20 см ; C x = 1.

По формуле ( 29) найдем напряжения :

на поверхности покрыти я

на подошве

На подошве возникнут напряжения растяжения при изгибе , а на поверхности - напряжения сжатия при и з гибе .

Пр имер 2 . Найти температурные напряжения в 14 часов на подошве плиты при невозможности коробления и волновом распределении температуры по тол щ ине .

Дано : E = 350000 кгс / см2 ; α = 10-51/° С ; h = 20 см ; C x = 1 , T ( у , t ) по формуле ( 21); T ср = 26; A 0 = 12,6; a = 0 ,003.

Согласно указаниям п . 41 вначале найдем распределение температуры по толщине плиты . В примере 5 приложения 1 были най д ены T (20,14) = 27 , T ( 0,1 4) = 38,6. По формуле ( 21 ) найдем температуру на глубине 5, 10 и 15 см от поверхности . На глубине 5 см будем иметь :

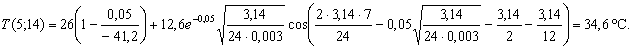
Аналогично найдем T (1 0,1 4) = 31,2 ° С и T ( 15,1 4) = 28,5 ° C .

Разобьем толщину плиты на 8 равных частей Δh = 2,5 см и п о и н терполяции найдем температуру в плите через 2,5 см . Значения температур ы приве д ены в т абл. 1.

Та б лица 1

T ( y ,14)

38,6

36,5

34,6

33

31,2

29,9

28,5

27,7

27

h , с м

0

2,5

5

7,5

10

12,5

15

17,5

20

y

y 0

y 1

y 2

y 3

y 4

y 5

y 6

y 7

y 8

По следующему правилу трапеций найде м значение интеграл а в формуле ( 25 ):

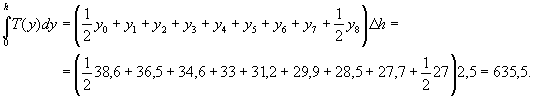
Температурные напряжения на подошве плиты найдем по формуле ( 29 ):

Из примера 2 следует , что

при гармонической функ ц ии температуры ( 21 ) н апряж ения на подошве плиты почти на 4 к гс / см2 меньше , чем при линейном перепаде температуры ( см . п ример 1) ;

средняя температура по к ры тия, рав ная 31, 7 = 635,5 : 20 и вызывающ ая продольные деформаци и плиты , боль ше температуры в срединной плоскости ;

изменение температуры по толщине покрытия в различные часы суток вы з ывает соответствующие и з менения температурных напряжений . Максимальные градиент ы температуры в покрытии , приближаю щ иеся к линейным , сохраняются в плите короткое время , которое в практ и ческих расчетах можно принять равным не более 1 ч .

Пр имер 3 . Найти температурные напряжения на подошв е плиты при частичной возможности коробления , волновом распределении температуры по толщине и расчетных параметрах примера 2 .

Расчет температурных напряжений произведем по формуле ( 32) с коэффициенто м меры коробления C x = 0 , 6. Сумма первых двух членов правой части , в формуле ( 32 ) б ыла найдена в примере 2 и ра вна -1 6,4 5 к г с / см2. Для нахождения интегра л а третьего члена воспользуемся правилом трапеций . С этой целью разобьем толщину плиты на восемь равных час те й Δh = 2,5 см , найдем ординаты каждой части поды н тегральн ой функции   и запишем значения ординат в табл . 2.

Таблица 2

y

y 0

y 1

y 2

y 3

y 4

y 5

y 6

y 7

y 8

h , см

0

2, 5

5

7,5

1 0

12,5

15

17,5

20

386

273

173

83

0

-75

-142

-208

-270

Примеч ание . Значения функции T ( y ,14) взяты из табл. 1 примера 2. Интеграл третьего члена опре делим по правилу трапеций:

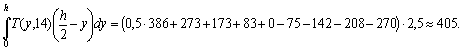
По формуле ( 32) получим :

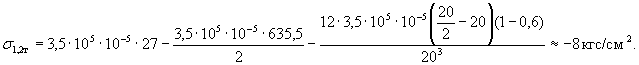
Сравнение примеров 2 и 3 показало , что у к орочение плиты ( C x = 0,6) уменьшает напряжения р астя жения при изгибе на подошве плиты до 8 кгс / см2 вместо 16,45 кгс / см2 при C x = 1.

Приложение 4

Примеры расчета температурных деформаций плит и швов

Пр имер 1 . Найти продольную температурную деформа ц ию плиты при суточном изменении температуры в перио д от 14 часов до 4 часов следующих суток в июле .

Дано : T ( y , t ) выражена формулой ( 21); T ср = 26 ° С ; A 0 = 12 , 6 ° С ; a = 0, 003 ; h = 20 с м ; φ 0 = 0 ; α = 10-51/ °С ; l = 6 м .

Расчетные параметры T н и T к определим по формулам ( 37).

В примере 2 приложения 3 была найдена T н = 31, 2 ° С . Для определения T к найдем распределение тем п ературы по толщине ( через 2,5 см ) по форму л е ( 21 ) . То г да температура поверхности в 4 часа при t = 14 ч равна :

Аналогично найдем температуру по тол щ ине плиты , результаты расчета которой приведены в таблице .

y

y 0

y 1

y 2

y 3

y 4

y 5

y 6

y 7

y 8

h , с м

0

2,5

5

7,5

10

12,5

15

17 , 5

20

Т ( y ,4 )

15,2

16,2

17,2

18,3

19,6

20,7

21,9

22,6

23,3

По правилу трапеций выч и слим интеграл и T к :

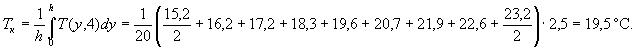
Теперь найдем деформацию плиты по формуле ( 33):

Δ l т = 10-5 · 6 00(31,2 - 19,5) ≈ 0 ,07 см .

Пр имер 2 . Найти ширину паза шва сжатия в покрытии , расположенном в д вух разных климат ич ески х районах . Для заполнения паза принята мастика одинакового состава .

Дано : α = 10-5 1/ ° С ; l = 5 м . В первом районе T н = 20 ° С , T к = - 1 0 ° С и предель н ая относительная д еформация растяжения мастики равна ε1 = 0,3. Во втором районе T н = 20 °С , T к = - 30 ° С и ε2 = 0,20.

Очевидно , предельные относительные деформа ц ии ε1 и ε2, соответствующие условиям разрыва масти ки или отрыва мастики от стенки паза , должны быть разные . Причем ε1 > ε 2 , так как с понижением температуры увеличивается модуль упругости мастики . В этом примере пре д полагается , что предельные относительные д еформации мастики установлены в ре з ул ьта те испытаний с учетом ее выносливости , старения и поперечного сечения мастики в пазе шва .

Относительные деформации мастики в шве εм и шва ε т равны

                                              ( 1)

где b - ширина шва ;

к - коэффициент увеличения температурной деформации шва всле д ствие несовпадения физической и геометрической середин плит , наибольшее значение которого равно 1 ,4 5 ( с м . п . 45).

Для обеспечения предельного растяжения масти к и в шве левые части выражений ( 1) д олжны быть равны , что позволяет из равенства правых частей найти ширину паза шва :

 откуда                                    ( 2)

По формуле ( 2) получим ширину паза шва :

в первом районе

во втором районе :

Если швы раскрываются одинаково , то к =1,0; b 1 = 5 м м и b 2 = 12,5 мм .

СОДЕРЖАНИЕ

Предисловие . 1

Общие положения . 1

Расчет температурных полей в цементобетонных покрытиях . 2

Расчет температуры поверхности покрытия . 5

Расчет распределения температуры по толщине покрытия . 6

Расчет температурных напряжений в бетонных покрытиях . 8

Приложения . 12

Приложение 1 Примеры расчета температуры покрытия . 12

Приложение 2 Применение практического гармонического анализа при расчете температуры покрытия . 14

Приложение 3 Примеры расчета температурных напряжений в покрытии . 17

Приложение 4 Примеры расчета температурных деформаций плит и швов . 18