Рекомендации Методические рекомендации по определению состава, состояния и свойств грунтов сейсмоакустическими методами
МИНИСТЕРСТВО ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА
ВСЕСОЮЗНЫЙ ОРДЕНА ОКТЯБРЬСКОЙ РЕВОЛЮЦИИ
НАУЧНО - ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУ Т
ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА
УТВЕРЖДАЮ
Зам. директора института
Н . Б . Соколов
2 апреля 1 985 г.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ОПРЕДЕЛЕНИЮ СОСТАВА,
СОСТОЯНИЯ И СВО Й СТВ ГРУНТОВ
СЕЙСМОАКУСТИЧЕСКИМИ
МЕТОДАМИ
Одобрены Главтранспр о ектом
Москва 1 985
ПРЕДИСЛОВИЕ
В настоящей работе приведены рекомен д ации по проведению сейсмоак устических работ при из учении разрезов нескальных грунтов и определению их физико-механических характеристик. Особое внимание уделено производству работ с поперечными волнами, наблюдению во внутренних точках среды и оценке состава, состояния и свойств грунтов. Учтена специфика изысканий под транспортные сооружения, приведены основные разработки ЦНИИСа по данным вопросам.
Методические рекомендации предназначены для геофизиков-сейсморазведчиков, а также инженеров-геологов, знакомых с основами сейсмоакустики.
Ме тодические рекомендации разработали инж. О. П. Аникин - гл. 1, 2, 3 (пп. 3.1, 3.13- 3.24) и 4, канд. г еол.- минерал. н аук Ю. В. Г оршенин - гл. 3 (пп. 3.2- 3.12) и приложение.
Зав . о тделением
изысканий и
проектирования железных дорог
А.М. Козлов
1. ОБЩИЕ ПОЛОЖЕНИЯ
1 . 1. Под сейсм оакустикой следует понимать комплекс разн очастотны х методов, основанных на использовании упругих волн: сейсмических - на частотах от 30 до 50 0 Гц, акустических - на частотах от 0,5 до 10 кГц, ультразвуковых - на частотах более 10 кГц.
1.2. Изучение строения разреза и описание кинематики распространения упругих волн в реальных средах основывается в данной работе на линейной теории упругости, согласно которой в однородной изотропной среде при динамическом воздействии на нее в какой-либо точке возникают два вида объемных волн: продольные - сжатия Р и поперечные - сдвига S .
Со свободной поверхностью связано существование поверхностных волн Релея и Лява [ 1 , 2]. Скорости упругих продольных Vp и поперечных Vs волн приведены в табл . 1.
1. 3. В качестве характеристики поглощения выбран декремент поглощения волн ν , который для значительных интервалов частот или слабо зависит от частоты колебаний, или совсем не зависит от нее [ 2, 3] и определя ется по формуле
ν = α · λ , (1)
где α - коэффициент поглощения;
λ - длина волны .
Амплитуда волны на разных удалениях от источника колебаний при совместном действии факторов расхождения и поглощения определяется по формуле
![]() , ( 2)
, ( 2)
где A ( x ) - амплитуда волны на расстоянии x от некоторой начальной точки;
A 0 - амплитуда волны в начальной точке;
e - натуральный логарифм;
τ - показатель расхождения.
Таблица 1
|
Типы грунтов |
Vp, м/с |
Vs, м/с |
Vs / Vp |
|
Неводонасы щенны е: |
|
|
|
|
валунно-галечные отложения |
500-10 00 |
250-500 |
0, 60- 0,70 |
|
пески |
200-500 |
150-300 |
0, 50- 0,70 |
|
супеси |
250-700 |
150- 400 |
0,45-0,60 |
|
суглинки |
300-1000 |
150- 500 |
0, 30- 0,55 |
|
глины (включая коренные) |
400-18 00 |
200-600 |
0,15-0,35 |
|
Водонасыщ енны е: |
|
|
|
|
валунно-галечные отложения |
2000-2700 |
250-500 |
0, 10-0,20 |
|
пески |
1500-2000 |
150-300 |
0,10 -0,18 |
|
супеси |
1500-18 00 |
150- 400 |
0,10 -0,20 |
|
суглинки |
1500- 1900 |
150- 500 |
0,10- 0,25 |
|
глины (включая коренные) |
18 00-2500 |
200- 600 |
0,10 -0,25 |
В реальных средах на амплитуду волн влияет также неоднородность среды, вследствие чего определяемые на практике пока з атели поглощения следует считать, строго говоря, эффективными величинами.
1.4. Главной особенностью сейсмоакустических исследований, которую следует учитывать при определении состава, состояния и свойств грунтов, является необходимость определения истинных значений сейсмических характеристик как продольных, так и поперечных волн даже в тех случаях, когда для расчленения разреза можно обойтись только одним , обычно продольным, типом волн.
Спецификой изысканий под транспортные сооружени я являются более высокие требования к портативности аппаратуры и оборудования и сложность подбора способов и уравнений расчета физико-механических свойств грунтов по относительно малому опорному материалу.
1.5 . Задачами сейсмоакустических исследований при изучении массивов нескальных грунтов для определения их свойств, состава и состояния являются:
расчленение геологического разреза (определение числа и мощности слоев , конфигурации границ);
определение сейсмоакустических характеристик для выделенных толщ грунтов;
определение свойств, состава и состояния нескальных грунтов.
1.6. При изучении разрезов нескальных грунтов следует применять:
сейсмические наземные измерения;
вертикальное сейсмическое профилирование и каротаж;
ультразвуковые измерения в естественных условиях и на образцах пород.
2. ПРОИЗВОДСТВО РАБОТ
Аппаратура и методика наземных сейсмических измерений
2.1. Сейсмическая аппаратура должна выбираться в зависимости от вида измерений, строе н ия сейсмогеологич еского ра з реза, характера решаемых задач и категории местности. Основные типы регистрирующей аппаратуры, рекомендуемой для выполнения работ, и ее характеристики приведены в табл. 2.
При изучении сложных разрезов для регистрации волн в первых и последующих вступлениях предпочтение должно быть отдано многоканальным отечественным сейсмическим станциям типов "П оиск-1 -6/1 2" , АСМ-ОВ, СМОВ-24 и зарубежным - ИСН-01 , Mc Seis -1300.
Малоканальные сейсмические установки обладают значительно меньшими возможностями и применяются в основном при наблюдениях по методу первых вступлений для решения простейших задач (например , изучения границ, связанных с уровнем грунтовых вод или поверхностью коренных глин).
2.2. Измерения следует производить способом продольного профилирования на единичных профилях или их системе. Непродольное профилирование используют редко , так как оно не гарантирует точных количественных построений, поэтому в настоящих Методических рекомендациях не рассматривается.
2.3. При сложном строении разреза (например , инверсионном распределении скоростей и неполном экранировании) пункт возбуждения колебаний рекомендуется заглублять. Обычно это делается с помощью взрывов в буровых скважинах, что относительно сложно и дорого. Как показал опыт ЦНИИС, более экономичным и технически доступным является использование для этой цели портативной установки динамического зондирования (и з комплекта ЭДЗ ЦНИИС [ 4] ).
2.4. Методика наземной сейсморазведки на продольных волнах достаточно полно освещена в литературе [ 5 , 6 , 7 и др.] . Поэтому в этом разделе рассматриваются лишь особенности производства работ с поперечными и поверхностными волнами, менее освоенными в технико-методическом отношении.
Т а блица 2
|
Аппаратура |
Число каналов |
Полоса пропускания, Гц |
Точность отсчета времени, мс |
Накапливание сигнала |
Регистрация |
Динамический диапазон, дБ |
Чувствительность, мм/мкВ |
Потребляемая мощность, Вт |
Масса, кг |
|
МАЛОКАНАЛЬНАЯ: |
|
|
|
|
|
|
|
|
|
|
ОСУ-2 |
1 |
20-600 |
0,1 |
Нет |
Аналоговая на ЭЛТ с фикси рованием на ф отопл енку |
- |
2 |
1 0 |
7 |
|
ДОСУ -1 |
2 |
20-1 000 |
0,1 |
-«- |
То же |
1 20 |
4 |
13 |
1 6 |
|
СНЦ -1 |
1 |
1 0-1 000 |
0,1 |
Цифровое |
Аналогов ая на ЭЛТ и элек троэррозионную бумагу |
60 |
4 |
15 |
15 |
|
Bison 1 550 (США) |
1 |
5-2000 |
0, 01 |
-«- |
Аналоговая на ЭЛТ |
- |
- |
3 |
5 |
|
МНОГОКАНАЛЬНАЯ: |
|
|
|
|
|
|
|
|
|
|
П оиск -1 -6/1 2 АСМ-ОВ |
1 2 |
1 5-1 25 |
0,5 |
Нет |
Аналоговая на магнитную ленту и фотобумагу |
40 |
20 |
1 20 |
1 50 |
|
Поиск-1 -24 М ОВ-О В |
24 |
1 5-1 20 |
0,5 |
-«- |
То же |
46 |
20 |
300 |
250 |
|
СМ ОВ-0-2 4 |
24 |
1 0-1 20 |
1 ,0 |
Аналоговое |
Аналоговая на магнитную ленту с восп роизведением на б умагу |
- |
- |
70 |
- |
|
ИСН-01-024 (В НР) |
24 |
20-2000 |
0,1 |
Циф ровое |
Цифровая на м агни тную ленту и аналоговая на электроэррозионную б умагу |
9 6 |
- |
1 00 |
50 |
|
Мс Seis -130 0 (Япония) |
24 |
5-1000 |
0,5 |
Циф ров ое неог ра ничен ное |
Аналоговая на бумагу с ультрафиолетовым проявлением |
86 |
- |
60 |
1 6 |
2.5. В методике работ с поперечными волнами имеются две принципиальные трудности , которые следует учитывать при проведении исследований:
получение чистых записей поперечных волн, не осложненных присутствием продольных волн, находящихся в первых вступлениях;
возбуждение поперечных волн достаточной интенсивности.
Первое имеет место в ближней (1-3λ) к ПВ зон е, второе - при значительной глубине исследований.
2.6. Из поперечных волн рекомендуются в первую очередь волны типа S H , которые возбуждают горизонтальными ударами по вертикальной стенке ямки или торцу прикопанного бревна в направлении, перпендикулярном ли нии профиля (п о оси Y ), и принимают горизонтальными (по оси Y ) сейсмопр и емн иками. Для опознания волн типа SH следует получать записи с противоположно направленным и ударами, за счет чего поперечная волна меняет фазу на противоположную, а продольная волна - нет.
Однако направленность источников возбуждения (особенно типа сосредоточенной силы ) и сейсмоприемников такова, что одновременно с волнами типа S H на записях (в ближней к ПВ зоне) присутствуют довольно интенсивные волны типа Р.
2.7. Для подавления продольных волн на записях поперечных следует осущ е ствлять фильтрацию колебаний, так как спектр колебаний продольных волн является более высокочастотным, чем поперечных, и ограничение спектра со стороны высоких частот (применение ФН Ч) значительно ослабляет или даже подавляет первые из них.
2.8. В тех случаях , когда возбуждение поперечных волн типа S H с помощью кувалды не обеспечивает необходимой интенсивности колебаний, следует применять специальные ударные устройства [ 8, 9] .
В качестве одного из таких источников возбуждения поперечных волн рекомендуется маятниковое устройство конструкции Ц НИИС для нанесения горизонтальных касательных ударов (рис. 1). Цилиндрической формы наборный груз 1 массой 15-50 кг подвешивается на стержнях 3 к горизонтальной оси 10, удерживаемой муфтами 13 на двух опорных ногах треноги 7 на высоте 2 м. Груз на рабочую высоту (до 2,5 м) поднимается ручной лебедкой 9, трос 8 от которой через блок 6 треноги 7 и несущи й рычаг 4 специальным захватом 2 крепится к грузу 1. Несущий рычаг удерживает груз при подъеме. С помощью спускового шнура 5 захват 2 размыкается, и груз начи нает двигаться вниз в вертикальной плоскости до нанесения удара по подставке 11 . Конструкция блока сочленения 12 стержней 3 груза с горизонтальной осью 10 обеспечивает возможность некоторого перемещения груза в плоскости, горизонтальной оси (п ерпендикулярно нанесению удара), благодаря чему груз движе тся вертикально и ослабляется боковая вибрация треноги.
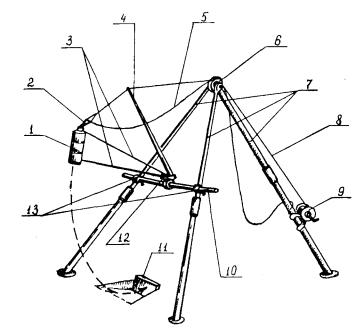
Рис. 1. Маятниковое устройство для возбуждения поперечных волн
2.9. В качестве нового высокоэффективного источника возбуждения поперечных волн рекомендуется скважин ное устройство, применение которого обеспечивает высокую чистоту возбуждения поперечных волн пр и низком уровне продольных. Схематическая конструкция под обного устройства, используемого в ЦНИИСе, показана на рис. 2. Оно состоит из металлических контактных щек 1, де ревянных прокладок 2, распорной воздушной камеры (с подводящим шлангом) 3, металлического диска 4. При работе устройство опускается в лунку или мелкую скважину таким образом, чтобы над поверхностью выступала часть его высотой примерно 20 см.
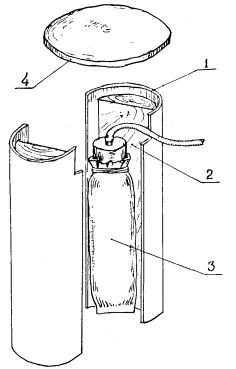
Рис. 2. Сква жи нное устройство для возбуждения поперечных волн
Ручным насосом создается давление в распорной камере , в результате чего она увеличивается в объеме и через прокладки давит на контактные щеки, плотно прижимая их к стенкам лунки. На торцы контактных щек кладется металлический диск 4, по которому наносятся удары молотком или кувалдой.
Длины , поперечные размеры и давление в камере след ует выбирать в зависимости от мощности источника, условий бурения лунок или скважин и транспортировки. Как показал опыт ЦНИИС, оптимальными параметрами устройства являются следующие: длина контактных щек 80-100 см , диаметр 15-20 см, давление в распорной камере 0,3 -0,5 МПа . Они обеспечивают в большинстве случаев глубину исследований до 10 м. Контактные щеки удобно изготавливать из отрезка трубы указанных размеров, разрезав ее по длине на две части. Кожухом распорной камеры может служить пожарный рукав, а внутренняя воздушная камера склеивается из резины. Давление в камере контролируется простейшим манометром.
Лунки глубиной до 1 м рекомендуется бурить ручными бурами (типа садо в ого или ш некового ледобура).
2.10. При глубине исследований , п ревышающей 10 м, длина установки должна составлять 1,5 -2,0 м, а давление в камере - 0,7 -0,8 МП а. Удары по накладному диску осуществ ляют падающим грузом разной массы.
Вместо одного большого устройства могут быть применены два малых, состыкованных последовательно друг за другом в скважине по глубине.
2.11. Для возбуждения с помощью скважинного устройства поперечных волн типа SH следует бурить наклонную (в плоскости ZY ) лунку с отклонением от вертикали на 30-45°. Колебания возбуждают ударами кувалды вдоль оси устройства, прием осуществляют горизонтальн ыми сейсмоприемн иками, ориентированными по оси Y . Если нужно получить записи с противоположной поляризацией удара, следует бурить другую лунку с отклонением от вертикали в противоположную сторону .
При данной методике работ обеспечиваются максимальная чистота записи поперечных волн и их надежное опо з навание, в связи с чем отпадает необходимость в низкочастотной фильтрации колебаний.
2.12. Наибольший эффект при при м енении скважинного устройства достигается при работе с поперечными волнами типа SV в случае возбуждения и приема колебаний по системе ZZ , при этом отпадает необходимость в замене вертикальных сейсмоприемников горизонтальными при переходе от регистрации продольных волн к поперечным. Не вызывает трудностей и обеспечение необходимой интенсивности колебаний.
Чистота записей волн типа S V достаточно высока , хотя и несколько хуже, чем волн типа SH . В некоторых случаях для подавления продольных волн рекомендуется осуществлять фильтрацию колебаний.
2. 13 . Работу с поверхн ос тным и волнами типа Релея и Лява рекомендуется проводить лишь в тех случаях, когда трудности методического характера не позволяют получить качественные записи поперечных волн ввиду относительной сложности и трудоемкости измерений, а также более низкой надежности и точности результатов. Эти измерения могут дать информацию о скоростном (для волн) строении среды примерно до глубины 10 м при условии ее градиентного характера.
Аппаратура и методика работ подробно освещены в литературе [ 10]. Следует отметить, что для уверенного и детального освещения разреза необходимы записи первых низших гармоник волн на пяти или более отличающи й ся частотах в диапазоне 5-70 Гц. Каждая гармоника имеет свой интервал регистрации, где она разрешена во времени с другими волнами и достаточно интенсивна. Волны Релея наблюдают по системе ZZ , Лява - по системе YY .
Аппаратура и методика наблюдений во внутренних точках среды
2.14. Наблюдения во внутренних точках среды наиболее эффективны при изучении скоростного строения разреза , так как они позволяют исследовать разрезы с люб ым распределением скоростей, в том числе и инверсионным, когда их изучение наземными сейсмическими методами затруднено или невозможно.
2.15. Вертикальное сейсмич ес кое профилирование в скважинах (ВСП), к ак сухих, так и заполненных водой, рекомендуется выполнять с помощью многоэлементных сейсмических зондов и многоканальных (более 12) сейсмостанц ий (см. т абл. 2). Для уверенной регистрации продольных и поперечных волн каждый приемный элемент должен состоять из вертикального и горизонтального приборов. Необходимое качество записи ( особенно для поперечных волн) обеспечивается плотным прижатием каждого элемента к стенке скважины.
2.16. Количество пунктов возбуждения (ПВ) и их удаление от устья скважины зависят от предполагаемого способа интерпретации.
Если количественная интерпретация предполагает приведение непродольны х наблюдений к продольным, то первый ПВ располагается вблизи устья скважины и два других - на расстояниях 0,3 Н и 0,5 Н, но не далее 10 м, где Н - глубина скважины [ 11, 12].
Когда интерпретация проводится без приведения непродольных наблюдений к продольным, то первый ПВ располагается также у устья скважины, а два других - на расстояниях примерно 0,5 Н и 1 ,0 Н , но не далее 20 м.
Если предполагается построение поля изохрон, то ПВ удаляются на 2-3 Н.
Следует учитывать также, что поперечная волна разрешена на записях во времени с продольной лишь в тех случаях, когда ПВ удален от скважины на 3-5 м и более.
2.17. Методика возбуждения и приема волн при ВСП ана л огична методике при наземных наблюдениях (с м. п п. 2.4- 2.12). На системах ZZ наблюдают продольные и поперечные волны типа S V , на системах YY - поперечные волны типа SH . Более высокочастотными на записях поперечных волн являются волны типа SV .
При относительно малых удалениях П В от устья сква жин ы (мене е Н) регистрация продольных и поперечных волн типа SV уверенно осуществляется и по системе ZZ , в связи с чем при больших объемах работ экономически целесообра зно применение многоэлементного сейсмического зонда с вертикальными сейсмоприемниками .
2 .18 . Сейсмический каротаж скважин , являющийся частным случа ем ВСП (регистрация первых вступлений), рекомен дуется выполнять с помощью одного-, двухэлементного зондов и малоканальных сейсмически х установок. Обычно наблюдения ведут на продольных волнах. За счет высокой точности ре гистрации времен указанной аппаратурой, особенно нового поколения (с м. т абл. 2), достигается высокая разрешающ ая способность метода при расчлене нии разрез а и определении скоростей. Шаг наблюдений в неводонасы щенны х породах в некоторых случаях целесообразно уменьшать до 25 см.
Регистрация волн типа S в принц и пе также возможна при условии подавления продольных волн. Волновую картину лучше фи ксировать для последующего камерального анализа.
Аппаратура и методика ультразвуковых измерений
2.19. Ультразвуковые измерен и я на образцах грунта и в массиве проводят с помощью импульсной аппаратуры, рассчитанной обычно на питание от сети переменного тока (табл. 3). Измерения в полевых условиях рекомендуется выполнять аппаратурой с автономным питанием типов УК-1 0П и Р-5-5 (последняя требует специальной пе ределки [ 13]).
2.20. Изм е ре ния осуществляют по методике продольного профи ли ровани я и просвечивания [ 14].
Табли ц а 3
|
Параметры |
Единицы измерения |
Тип прибора |
||||||
|
ДУК-20 |
УКБ -I |
УКБ -II |
ПИК-ТОМ |
УЗС-260 |
ИПА-59 |
УК-10П |
||
|
П олоса п ропускани я |
кГц |
1 -500 |
5-3 0 0 |
5-220 |
1 0- 200 |
15 - 300 |
1 0-500 |
1 0-1 50 |
|
Коэф ф ициент усиления |
10 6 |
1 |
0,5 |
1 ,1 |
0,8 |
1 |
0,37 |
0,5 |
|
Чувствительность |
м кВ |
50 |
1 0 |
50 |
1 00 |
- |
- |
5 |
|
Длительность развертки |
мкс |
20 |
1 00 |
1 2 |
1 0 |
1 00 |
50 |
50 |
|
мс |
- |
1 0 |
1, 5 |
4 |
2 2 |
1 2 |
1 ,5 |
|
|
Основные ме тки в ремени |
мкс |
1 |
1 0 |
1 |
2 |
1 0 20 |
1 0 |
1 |
|
Амплитуда зондирующих импульсов |
кВ |
0,25 0,50 |
0,70 |
0,4 |
0 , 30 |
1 |
0,40 0,80 1 ,60 |
0,25 |
|
Размеры экрана Э ЛТ |
см |
1 3 |
8 |
8 |
8 |
3 1 |
1 3 |
8 |
|
Масса прибора |
кг |
45 |
1 5 |
1 4 |
28 |
- |
1 8- 37 |
8,5 |
|
Потре б ляемая мощность |
Вт |
500 |
1 40 |
24 |
1 70 |
- |
200 |
30 |
3. ОБРАБОТКА И ИНТЕРПРЕТАЦИЯ МАТЕРИАЛОВ СЕЙСМОАКУСТИЧЕСКИХ НАБЛЮДЕНИЙ
3.1. Процесс обр а ботки и ин те рпрета ци и материа лов сейсмоакусти ческ их наблюдений, осуще ств ляемый дл я определения глубин сейсмически х границ и ли мощ носте й слоев и скоростей распростране ния в них упругих волн, включает визуализацию материа лов, и х марки ров ку и оценку качества, корреляцию волн и установ лени е их природы, построение годографов и их и нтерпретацию на основе принятой сейсмической модели . Эти вопросы, а также вопросы, касающиеся определения декрементов поглощения волн, достаточно полно освещены в литературе [ 5 , 6 , 7 , 14 , 15 , 16 и др.], поэтому в настоя щ их Методических рекомендациях они не рассматриваются. В раз деле приводятся лишь те данные, которые имеют частое употребление на практике или слабо освещены в ли тературе.
Обработка и интерпретация материалов наземных наблюдений
3.2. Количественную интерпретацию следует выполнять по материалам продольного сейсмического проф или рования.
В случае параллельности нагоняемого и нагоняющего годографов ра з рез следует отождествлять со слоисто-однородной средой, а зарегистрированные волны считать преломленными. В случае непараллельности указанных годографов (при отсутствии проницания) разрез следует отождествлять с градиентной средой, а волны относить к рефраги рованны м.
Интерпрета ция годографов пр еломленных волн
3.3. Граничные скорости определяются несколькими способами [ 5 , 6 , 7 , 14 , 17 ]. В инженерной сейсморазведке рекомендуется применять способ разностного годографа , основанного на использовании выражения
![]() , (3)
, (3)
где ![]() и
и ![]() - вр е мена по встречным годографам
- вр е мена по встречным годографам ![]() и
и ![]() в точке x профиля наблюдений;
в точке x профиля наблюдений;
T - взаимное время.
Разностный годограф θ( x ) обычно строят графически (рис. 3). В тех случаях, когда встречные годографы не увязаны во взаимных точках, построения ведут от любой условной линии, параллельной оси абсцисс (расстояний). Граничная скорость V Г определяется по разностному годографу из выражения
![]() , (4)
, (4)
где φ - угол наклона преломляющей границы, рассчитываемый по формуле
![]() . ( 5 )
. ( 5 )
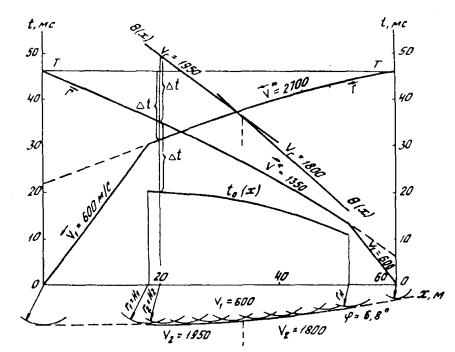
Рис. 3. Опре де ление граничных скоростей и положения преломляющей границы по встречным годографам
Здесь
![]() - средняя скорость в
покрывающей толще до границы;
- средняя скорость в
покрывающей толще до границы;
![]() ,
, ![]() -
кажущиеся скорости на границе из встречных ПВ.
-
кажущиеся скорости на границе из встречных ПВ.
Если на интервале определения V Г наклон преломляющей границы не более 15°, то граничная скорость с погрешностью, не превышающей 10 %, может определяться п о упрощенной формуле
![]() . (6)
. (6)
Способ тем точнее, чем больше перепад скоростей на границе раздела.
3.4. Если участок перекрытия у встречных годографов отсутствует, значение V Г приближенно определяется для всего интервала между ПВ по формуле
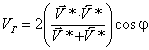 . (7)
. (7)
Если имеется лишь одиночный годограф , величина V Г приближенно принимается рав ной V * .
3.5. Когда по каким-либо причинам получение записей поперечных волн связано со значительными трудностями и неудобствами или эти записи просто отсутствуют, скорость поперечных волн Vs верхней части раздела можно определять через скорости релеевских VR и продольных Vp волн с помощью палетки Кнопова (р ис. 4) . При этом отпадает необходимость в дополнительных записях по системе YY , так как релеевские и продольные волны регистрируются вместе на одной сейсмоленте , полученной по системе ZZ .
3.6. Построение преломляющих границ в инженерной сейсморазведке осуществляют в большинстве случаев способами средних и пластовых скоростей , используя параметр t 0 [ 5, 6, 7, 14, 17]. Посл едний определяют по формуле
![]() , ( 8 )
, ( 8 )
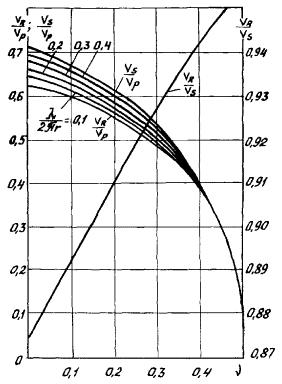
Р ис. 4. Номограмма К нопова-К оптев а для определения коэффициента Пуассона по скоростям волн.
Параметр кривых λ/2π r , где r - радиус выработки
Обычно это делают графически на участках перекрытия встречных годографов (с м. р ис. 3). Дополнительно приближенные з начения t 0 находят в точках ПВ путем про должен ия (пунктирные линии) годографов до пересечений их с осью времен. При этом встречные годографы одноименной волны должны быть обяз ательно увязаны по времени во взаимных точках. Если встречные годографы не имеют участка перекрытия или имеется только один годограф, то значение t o находится приближенно (пунктирные линии) по отрезку, отсекаемому на оси времен при продолжении годографа (рис. 5). Глубина залегания преломляющей границы в способе средних скоросте й или мощность пласта в способе средних скоростей или мощность пласта в способе пластовых скоростей могут быть найдены во всех точках профиля, где известны значения t 0 .
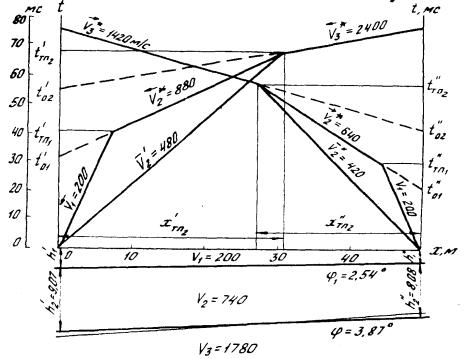
Рис . 5 . Интерпретация годографов трехслойного разреза при отсутствии участков их перекрытия
Определение глубины до преломляющих границ по единичным годографам можно выполнять также по абсциссе точек пересечения ветвей годографов без использования t 0 .
3.7.
При способе средних ско ростей для определения
глубины преломляющей границы нужно з нать не только величины V Г и t 0 , н о также и
среднюю скорость ![]() в толщ е, лежащей выше границы.
Точную в еличину
в толщ е, лежащей выше границы.
Точную в еличину ![]() может дать сейсмокаротаж
или ВСП .
может дать сейсмокаротаж
или ВСП .
Для
нахождения средней скорости ![]() можно использовать ра з ведочные
скважины, расположенные на профиле наблюдений. Средняя скорость определяется по
формуле
можно использовать ра з ведочные
скважины, расположенные на профиле наблюдений. Средняя скорость определяется по
формуле
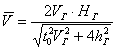 , (9)
, (9)
где H Г - глубина до преломляющей границы в месте расположения скважины.
Если
возбуждение волн производится на некоторой глубине Н дз (например ,
с помощью портативной установки динамического з ондирования), то средняя скорость ![]() до
промежуточной глубины h Г может быть
определена и з выражения
до
промежуточной глубины h Г может быть
определена и з выражения
![]() , (10)
, (10)
где Δ t - разность времен вступлений волны при возбуждении на поверхности и глубине h Г .
Угол i расс чи тывается из выражения
![]() , (11)
, (11)
где V 1 - скорость вблизи поверхности наблюдений (берется по годографу прямой волны при возбуждении на поверхности ).
В случае резкой границы, когда горизонтальным сносом можно пренебречь (например, УГВ), средняя скорость может быть определена по более простой формуле
![]() . (12)
. (12)
При
возбуждении колебаний на поверхности приближенная величина средней скорости для
К-й границы ![]() может быть получена
по точкам пересечения (ТП) годографов преломленных волн из выражения (с м. р ис. 5)
может быть получена
по точкам пересечения (ТП) годографов преломленных волн из выражения (с м. р ис. 5)
![]() , (13)
, (13)
где x тпк и t тпк - координаты точки пересечения годографов , соо тветствующие границе К.
Представление
о величине относительных ошибок определения средней скорости ![]() по точке пересечения
годографов для трехслойной гори з онтальной среды в зависимости от отношения V 1 / V 2 можно получить
из рис. 6. Параметром кривых
является отношение V 1 / V 3 . Случай, представленный на рис. 6, а , рассчитан для
отношения мощностей
по точке пересечения
годографов для трехслойной гори з онтальной среды в зависимости от отношения V 1 / V 2 можно получить
из рис. 6. Параметром кривых
является отношение V 1 / V 3 . Случай, представленный на рис. 6, а , рассчитан для
отношения мощностей ![]() = 1, а случай, показанный на рис. 6, б - для
= 1, а случай, показанный на рис. 6, б - для ![]() = 3.
= 3.
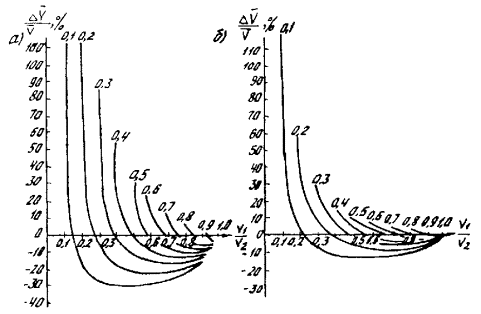
Рис. 6. Графики определения ошибок пр и расчете средних скоростей по координатам точки пересечения для трехслойного разреза
Глубина з алегания К-й границы определяется по формуле
![]() или
или 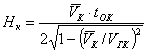 , (14)
, (14)
где 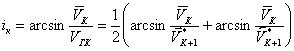 ; (15)
; (15)
![]() - ср е дняя
скорость в покрывающей толще до гра ницы К;
- ср е дняя
скорость в покрывающей толще до гра ницы К;
V ГК - гран ичная скорость на границе К;
![]() и
и ![]() - кажущиеся скорости волны
от границы (ветвь годографа К + 1) из встречных ПВ.
- кажущиеся скорости волны
от границы (ветвь годографа К + 1) из встречных ПВ.
В ч а стности, для первой преломляющей границы формулы ( 14) и ( 15) принимают вид:
![]() или
или 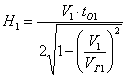 ; (16)
; (16)
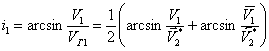 . (17)
. (17)
3.8. Способ пл астовых скорост ей является более точным, хотя и более трудоемким, чем способ средних с к оросте й. Он заключается в последовательном определении мощности каждого отдельного слоя hi (см . р ис. 5). При этом для каждой К-й границы определяют значения t ОК и V ГК согласно методике, изложенной в пп. 3.3 и 3.4.
М ощн ост ь пе рвого слоя h 1 , ра вн ого глубине Н1 до первой границы, определяют по формуле ( 16).
Мощность второго слоя h 2 находят из выражения
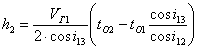 . (18)
. (18)
Глубина до второй границы H 2 = h 1 + h 2 .
Мощность третьего слоя h 3 определяют по в ы раж ению
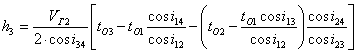 , (19)
, (19)
где i12 = arcsin V1/V2 = arcsin V1/V Г 1 ;
i13 = arcsin V1/V3 = arcsin V1/V Г 2 ;
i23 = arcsin V2/V3 = arcsin V Г 1 /V Г 2 ;
i14 = arcsin V1/V4 = arcsin V1/V Г 3 ;
i24 = arcsin V2/V4 = arcsin V Г 1 /V Г 3 ;
i34 = arcsin V3/V4 = arcsin V Г 2 /V Г 3 .
Глубина до третьей границы H 3 = h 1 + h 2 + h 3 .
Аналогичные
формулы су щ ествуют и д ля сл едующих слоев. Однако они
слишком громоздки и неудобны для практических расчетов. На практике при
определении мощ ности третьего и последующи х слоев применяют
комбинированный способ, при котором многослой ная
среда заменяется трехслойной, состоящей из
слоя, мощность ко торого
необходимо определить, подстилающего пласта и вы шележащей т олщи , объединенной в один
слой со средней скоростью ![]() . Положение кровли искомого пласта находят способом средних
скоростей, а его мощность - способом пластовых скоростей.
. Положение кровли искомого пласта находят способом средних
скоростей, а его мощность - способом пластовых скоростей.
3.9. Способ определения глубин по абсциссе точек пересече н ия рекомендуется применять при небольших перепадах скоростей на границе (0, 5 < VK / VK +1 < 1) и малых наклонах гран и ц.
Мо щ ность покрывающего слоя h 1 (с м. р ис. 5)
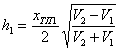 , (20)
, (20)
где x ТП1 - абсцисса точки пересечения годографов.
М о щность второго слоя
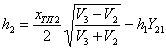 , (21)
, (21)
где
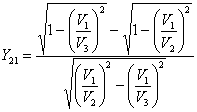 . (22)
. (22)
Ре з ультаты интерпретации годографов преломленных волн, приведенных на рис. 3 и 5, даны в приложении.
Интерпретация годографов реф раг ированных в олн
3.10. Большинство и з вестны х способов интерпретации годографов рефрагированны х волн применяется при залегании градиентного слоя на полупространстве и отсутствии скачка скоростей на границе сред (границе второго рода).
Интерпретация годографов рефрагированных волн сводится к отысканию закона изменения скорости волны в градиентном слое V = f ( h ) и мощности градиентной толщи H . Интерпр е таци ю следует осуще ств лять для каждого единичного годогра фа в отде льн ости.
3.11. Сущ е ствует довольно много способов интерп ретации годографов рефра гированны х в олн [ 6, 7, 14, 17 и др.]. Учитыв ая относительн ую трудое мкость процесса и нтерпретации, при ручной обраб отке рекомен дуется применять относительно простые при бли же нны е методы. В и нже не рной сейсморазв едке ши ро ко апробирован и хорош о за рекоме ндов ал себя способ Конд ратье ва [ 17, 18] , в основе которого лежи т пре дставление градиентной среды как пред ельного случая слоист о-однородн ой среды при стремле нии мощности слоев последней к нулю.
Глубину проник н овения луча д ля выб ранной прои звольн ой точки годографа определяют по формуле (р ис. 7, а )
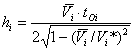 , (23)
, (23)
где ![]() - средняя
скорость в точке i ;
- средняя
скорость в точке i ;
tOi - значение времени , отсекаемое на оси времен касательной к годографу в точке i = 1 , 2, 3 ... т;
V * i - кажущаяся скорость в выбранной i -й точке с координатами ti , xi /2, равная истинной на глубин е максимального проникновения луча hi .
Среднюю
скорость ![]() вычисляют по
формуле
вычисляют по
формуле
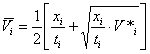 . (24)
. (24)
Для построения зависимости V = f ( h ) на годографе выбирают ряд точек и выполняют вычисления, описанные выше. Результаты всех вычислений Vi = V * i и hi заносят в таблицу, по которой строят график V = f ( h ) для да н ного участка наблюдений (см. р ис. 7, б).
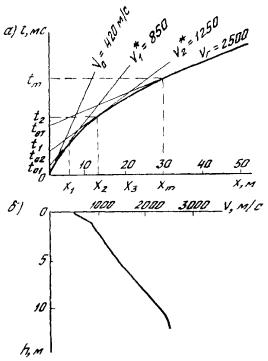
Рис. 7. Интерпретация годографа рефра г ированных в олн:
а - годограф волн с элементами
построений; б - соответствующ ий ему график
изменения скорости в зависимости от глуби ны
(по способу Кондратьева)
Для
с и льноградиент ной среды более точные результаты при вычислении ![]() получаются по
формуле, пред ложенн ой Павленк овой и
Смелянской [ 14, 19]:
получаются по
формуле, пред ложенн ой Павленк овой и
Смелянской [ 14, 19]:
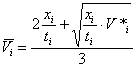 . (25)
. (25)
Интерпретация годографов р е фрагиров анны х волн для границы первого рода (скачка скоростей) более сложна и трудоемка, поэтому реже производится на практике [ 5, 7].
3.12. Для интерпретации годографов рефрагированных волн эффективно примен е ние ЭВМ. Наиболее полн ой в этой области являе тся программа "Грунт" для машины типа ЕС-10 20 на языке ФОРТРАН-1У [ 20 , 21 ].
3.13. Информация о величинах скоростей поперечных волн в градиентном разр е зе может быть получена по волнам Релея и Лява [ 10 , 20 ]. Точность и ра з решающ ая способность данного метода существенно ниж е, чем при использовании годографов поперечных волн, и находятся в прямой зависимости от числа фазовых годографов разных гармоник, получен ных в узких диапазонах низкочастотной части спектра (5-50 Гц).
Для количественной интерпретац и и в качестве ис ходных данных следует брать усредненные значения фазовых скоростей и периодов одной или нескольких ( обычно двух) низших гармоник волн Релея и Лява [ 10, 20]. Хорошие результаты получаются при значите льном (б олее пяти) числе наблюдений двух низши х гармоник указанных волн на сильн о различающихся частотах. Ма кси маль ная глубина исследований при этом составляет 10-12 м.
Ввиду большого объема вычислений практ и ческая реализация данного метода целесообразна с применением ЭВМ, для чего разработан ряд программ, в том числе программа "Г рунт".
Обработка и интерпретация материалов наблюдений во внутренних точках среды
3.14. Интерпретация материалов вертикального сейсмического профилирования сводится к определению скоростей продольных и поперечных волн в разр е зе по глубине и разд еле нию толщи на слои.
Полную информацию о распределении скоростей в р а зре зе следует получать из интерпретации продольных и непродольных в ертикальных годографов. Последние в большей степени рекомендуются для поперечных волн, так как непродольные системы обе спечив ают лучшее разрешение в о вре мени поперечн ой волны от продольной.
Наиболее просто й является интерпретация продольных год ографов, поэтому в большинстве случаев непродольные годографы рекомендуется приводить к продольным (к вертикали).
3.15. Приведение непродольных годографов к вертикали осуществляют обычно на основе модели однородной среды по формуле
![]() , (26)
, (26)
где h - глубина наблюдения;
S - расстояние от ПВ до устья скважины.
Приведение выполняют лишь для тех частей годографов, для которых выполняются условия h / S ≥ 0,3÷0,5 и S < 10, тем самым времена на приведенном годографе определяются с погрешностью , не превышающей 10 %.
3.16. Интерпретацию вертикальных продольных (или пр и веденных) годографов рекомендуется ос уществлять д вумя способами.
Согласно первому годограф осредн я ет ломаной линией, предполагая, что разрез сложен однородными слоями. Пла стовые скорости для каждого выделенного слоя определяют по угловым коэффициентам соответствующего отрезка ломаной линии.
Второй способ заключается в аппроксимации по частям вертикального экспериментального годографа элементом теорети чес кого годографа рефрагированны х волн вида [ 11]
t (h) = ah + bh2. (27)
Для этого в е сь годограф раз бивае тся на эле менты с числом точек в каждом из них 3-7 (в среднем 5). Для каждого элемента ра ссчитывают коэффициенты a и b по след ую щим формулам:
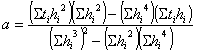 ; (28)
; (28)
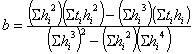 . (29)
. (29)
Скорость на данном интервал е г лубины (на элементе) вычисляют по формуле
![]() . (30)
. (30)
Данный способ позволяет восстанавливать скоростной ра з рез при любом законе изме нения скорости от глубины.
Имеется алгоритм и составлена программа "Обработка вертикального годографа с приведением" (ОВГП-1 ) д ля ЭВМ " Наири-2" [ 11, 12].
3.17. Интерпретация непродольных вертикальных годографов без приведения их к продольным более сложна и трудоемка, а по л учаемые результаты ненадежны [ 11, 12]. Поэтому этот способ обработки рекомендуется применять только в тех случаях, когда по каким-либо причинам непродольные годографы сложно привести к продольным.
Расчеты по непродольным годографам рекомендуется выполнять только с применением ЭВМ, для чего и мею тся соответствующие программы [ 20].
3 . 18. При наличии не скольких вертикальных н епр одол ьны х годографов со значительными удалениями ПВ от устья скважины ( S > h ) рекомендуется постро е ние поля и зохрон в плоскости S - h [ 5, 21]. Такое пред ставление результатов боле е рельефно подчеркивает скоростные особенности разреза. При этом б олее уверенно выделяются зоны с повышенными скоростями, чем с п ониженными.
Пример построения поля изохро н по непродольным в ертикальным годографам представлен на рис. 8.
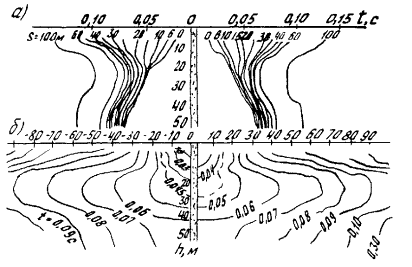
Рис. 8. Представление материалов вертикального профилирования через поле изохрон:
а - вертикальные годографы первых вступлений; б - поле изохрон, построенное по годографам на графике “ а” для воображаемого источника у устья скважины
3. 19 . Точность определения скоростей по годографам продольного и непродольного вертикального профилиров ания зависи т от качества экспериме нтальных годографов. Для того, чтобы погрешность в скоростях не превышала 10 % , значения времен на год ографах должны быть определены с точностью 0,0005-1,001 с.
Прибл и женная
количественная оценка относительной погрешности определения скорости ![]() в зависимости от
систематической ошибки во времени Δtφ / t , связанной с
неточной поправкой за фазу, выполняется из сл е дующих отношений [ 20]:
в зависимости от
систематической ошибки во времени Δtφ / t , связанной с
неточной поправкой за фазу, выполняется из сл е дующих отношений [ 20]:
а)
при занижении Δtφ (времена
годографа завышены) систематическая ошибка в скорост и ![]() ;
;
б) при завышении Δtφ (времена годографа занижены) систематическая ошибка в скорости гораздо больш е :
![]() ;
;
в)
наибольшая ошибка в скорости ![]() им е ет
место для глубин
им е ет
место для глубин ![]() .
.
Завышение времени на годографе приводит к с и стематическому занижению величин скоростей и наоборот.
Аналог и чная ошибка в скорости в зависимости от погрешности при определении р асстояния ПВ от устья скважины може т быть оц енена из соотношения [ 20].
Обработка и интерпретация материалов ультразвуковых наблюдений
3.20. Интерпретация данных ультразвуковых наблюдений (для прямых волн) выполня е тся по обычной системе и не вызывает затруднений [ 14, 22]. Скорость поперечных волн рекомендуется определять по скоростям продольных и поперечных волн с помощью палетки Кнопова (с м. р ис. 4) .
3.21. Предельную относительную ошибку в определении скорости при профилировании можно оценить из соотношения
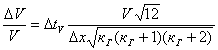 , (31)
, (31)
где V - скорость, рассчитанная по наклону годографа ;
Δx - расстояние между соседними положениями датчика на профиле (соседними точками на годографе );
кГ - чи сло точек на годографе;
Δ tV - предельная абсолютная ошибка определения в ремени по отношению к аппроксимирующей годограф прямой линии.
При прос в ечивании аналогичная ошибка в определении скорости находится из выражения
![]() , (32)
, (32)
где l - база просвечивани я;
Δl и ΔtV - абсолютные ош и бки в определении соответственно базы просвечивания и времени пробега волны.
Геологическая интерпретация сейсмоакустических данных
3.22. Отождествление сейсмических границ с геологическими и гидрогеологическими по сейсмическим данным следует производить: по форме записи волны на сейсмограмме, по форме годографов, по упругим и поглощающим характеристикам среды.
Дл я нескальных грунтов нужно учитывать при геологическом отождествлении границ степень водонасы щенности пород или их положение (выше или ниже) по отнош ению к уровню грунтовых вод.
3.23. Л и тологиче ск ие границы выше уровня грунтовых вод следует выделять на основе регистрации как продольных, так и поперечных волн либо их совместного использования. Качественную классификацию грунта можно сделать по величине отношения Vs / V p согласно табл. 4.
Таблица 4
|
№ п/п |
Грунт |
От но шение Vs / Vp |
|
1 |
Галечники |
0,60-0,68 |
|
2 |
Пески |
0,55-0,68 |
|
3 |
Супеси |
0 , 50-0,62 |
|
4 |
Суглинки |
0,30-0,55 |
|
5 |
Гли ны |
0,14-0,35 |
3.24. Литол о гически е границы ниже уровня грунтовых вод наиболее успешно отражаются на записях поперечных волн, и их скорости из меняются в более широком диапазоне, чем продольных (с м. т абл. 1 ) .
4. ОПРЕДЕЛЕНИЕ ФИЗИКО-МЕХАНИЧЕСКИХ СВОЙСТВ, СОСТОЯНИЯ И СОСТАВА НЕСКАЛЬНЫХ ГРУНТОВ
Выбор расчетных уравнений
4 . 1. Основными показателями свойств, состояния и состава нескальных грунтов, для оценки которых может использоваться сейсмоакустика, являются: модуль общей деформации E деф , у дельное сцепление С, угол внутреннего трения φ, плотность γ0 (плотность скелета грунта γск), пористость n (коэффициент пористости е ); влажность w , степень влажности g , п оказатель консистенции JL , число пластичности Wn и пределы пластичности W Г и Wp , гранулометрический состав - содержание глинистых (менее 0,005 мм) Г гл , пы леваты х (0,05-0,005 мм) Гпл и п есчаных (более 0,05 мм) Гпс частиц.
Упругие деформации и сдвиг при динамических нагрузках характеризуются соответственно динамическими модулями деформации Е g (модулем Юнга) и сдвига μ g , коэффициентом Пуассона νg .
4.2. Корреляционные уравнения связи, приводимые в настоящем разделе , справедливы при следующих размернос тях в ход ящ их в них параметров :
Vp и Vs м/с
φ град/см
E деф , Е g , C , μg МП а
γ 0 и γск г/см3
W и Г (гран состав ) % весовые
Wn , W Г и Wp % влажности
Ост а льные пара метры Безразмерные
Ук а зан ные разме рности необязательны (и в общем с лучае несправе дливы) для точных физических соотношен ий те оретиче ского характера. Для этих соот ношений разме рность параме тров зависит от выбранной фи зической системы еди ниц [ 23].
4 . 3. Для определе ния каждого параметра в большинстве случаев существует несколько способов расчета и расче тных урав нений. Выбор конкретного способа (или способов) и уравнения (или уравнений) зависит от необходимой точности и надежности определений, простоты и быст роты расчетов, наличия исходных сейсмических и д ругих данных о грунте и условий его залегания в разрезе. Правомочность выбранного способа расчета должна подтверждаться экспериментально.
4.4. По точности результатов, быстроте и простоте расчетов предпочтение следуе т отдавать простейшим корреляционным уравнениям (с числом исходных параметров, не превышающих двух), имеющим наибольш ее применение на практике. Среди ни х в свою очередь рекомендуются те частные зависимости, которые по типу пород, условиям их залегания и региону применения наиболее близки к каждому конкретному случаю.
Меньшее предпочтение следует отдавать корреляционным з а ви симостям, более региональным и универсальным п о типу пород. При этом обязательным является разделение грун тов на несвязные (с лабосвязные) и связные. Для первых из них региональный фактор не так важен по сравнению с типом грунта, для вторых он играет заметную роль.
Наиболее общие и универсальные корреляционные зависимости (для связных и несвязных грунтов всех районов СССР) не имеют пока необходимого экспериментального обоснования и вызывают определенные сомнения. Поэтому они могут быть использованы (особенно для связных грунтов) лишь для приближенной оценки соответствующих пар а метров и должны дублироваться другими способами расчета, учитывающими большее число факторов и физическую причинность св язей.
При выборе конкретного уравнения (уравнений) св яз и рекомендуется пользоваться графическим предста вле нием зависимости на одном планшете. Такие графики приведены в разделе по большинству анализируемых параметров .
4.5. В тех случаях, когда имеющиеся простейшие корреляционные зависимости не обеспечивают необходимой надежности определений (см . п . 4.4), р асчеты следует производи ть:
а) по более сложным многомерным (более двух) корреляционным уравнениям, включающим простейшие физические свойства, влияние которых на искомый параметр и сейсмические характеристики наиболее велико;
б) п о теоретико-э кспериментальным зависимостям, полученным на основе теоретических моделей грунта.
Необходимые дополнительные данные для первого случая (с м. подпункт а) следует получать из прямых инженерно- геологиче ских определений, а при их отсутствии - на основе сейсмических характеристик по системе замкнутых (число неизвестных равно числу уравнений) корреляционных многомерных уравнений в результате итераци онного процесса.
Во втором случае (см . п одпункт б) число исходных параметров увеличивают за счет использования помимо ско ростей волн также их декрементов поглощения (с пособ ЦНИИС) или путем контроля ряда параметров при расчете, причем технологиче ски наиболее удобны модель и способ В. И. Бондарева.
Указа н ные способы расчета носят более региональный и униве рсальный характер в силу более полного учета факторов, влияющ их на искомый параметр, и большей физической обоснованности д анн ого подхода. При этом, одн ако, увеличивается вли ян ие на конечный результат погрешностей в исходных параметрах по сравнению с использованием простейших урав нений.
4.6. При установлении новых зависимостей или проверке су щ ествующих соотношений необходимо, чтобы все сопоставляе мые параметры были получены в одинаковых инженерно-геологи ческих условиях с соблюдением масштабного эффе кта. Последне е относится к неоднородным грун там. Одн ородные грунты свободны от действия этого эффекта .
Определение механических свойств грунтов
4.7. Динамические модули деформации Е g и сдвига μg используют для решения специальных задач (р асчета ф ундаментов при динамических нагрузках и др.) и вычисле ния статически х характеристик грунта. Динамические модули вычисляют по известным функциональным зависимостям линейной теории упругости:
![]() ; (33)
; (33)
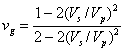 ; (34)
; (34)
![]() ; (35)
; (35)
где γ 0 - плотность грунта.
Таблица 5
|
Номер формулы и графика |
Типы грунтов |
Районы |
Уравнения связи |
Коэффициенты корреляции |
Пределы применения |
Авторы |
|
|
НЕСВЯЗН Ы Е И СЛАБОС ВЯЗНЫ Е ГРУНТЫ |
|
|
|
|
|
|
1 |
Вал унно- галечный аллювий с супе счан о-суглини сты м з аполнителем (н еводон асыщ енный) |
Все ра й оны СССР |
lg E деф = 1, 99 - lg E д - 3,66 |
- |
200 ≤ Едеф ≤ 480 |
В. Е. Лавров |
|
2 |
Щеб е нистые грунты (щебень та льк-хлоритовых сланц ев) |
-«- |
E деф = 0 ,1 E д - 16 |
- |
15 ≤ Едеф ≤ 130 |
В. И. Б ондаре в |
|
3 |
Су х ие и н еводон асыщ енные пе ски |
Зап а дная Сиби рь, Свердлов ск ая обл. |
E деф = 0 ,116 E д - 4,7 |
0,92 |
18 ≤ Едеф ≤ 66 |
В. И. Бондарев |
|
4 |
Пески неводонасы щ енные |
Все районы С С СР |
E деф = 0 ,085 E д + 3 |
0,84 |
15 ≤ Едеф ≤ 60 |
В. Н . Агеев |
|
5 |
-«- |
-«- |
E деф = 0 ,01425 Vp + 0,1985 Vs - 27 |
0,85 |
15 ≤ Едеф ≤ 60 |
В. И. Бондарев |
|
6 |
Пески в одон асыщенны е |
-«- |
E деф = 0 ,445 E д + 3,1 |
0,94 |
6,4 ≤ Едеф ≤ 80,7 |
В. Н. Агеев |
|
7 |
-«- |
-«- |
E деф = 0 ,15175 Vs - 18,9 |
0,92 |
6,4 ≤ Едеф ≤ 80,7 |
В. И. Бондарев |
|
8 |
-«- |
-«- |
E деф = 2,261· 10-4 V2s + 4,2 |
0,9 3 |
6,4 ≤ Едеф ≤ 80,7 |
В. И. Бон дарев |
|
|
СВЯЗНЫЕ ГРУНТ Ы |
|
|
|
|
|
|
9 |
Четвертич ны е суглинки неводон асыщенные |
Средн я я полоса Е вропей ской части СССР |
E деф = 0 ,0362 Eg + 2,6 |
- |
5 ≤ Едеф ≤ 16 |
О. П. А никин |
|
1 0 |
То ж е |
То ж е |
E деф = 0 ,0736 Vp + 0,0562 Vs - 3,7 |
- |
5 ≤ Едеф ≤ 16 |
О. П. Аник ин |
|
11 |
Суглинки |
Татарская ССР |
E деф = 0 ,33 E д + 6,5 |
- |
- |
И. Г. М инд ель |
|
12 |
Л е ссы и лессовидны е су глинки |
Юг Украин ы |
E деф = 0 ,045 E д + 7 |
0,8 1 |
8 ≤ Едеф ≤ 57 |
И. Г. Минд ель |
|
1 3 |
Суглинки кор ы выветривания |
Ср е дн еаму рска я впадина и ее обрамл ени е |
lg E деф = 0,57· 10-6 V2p + 2,42 |
0 ,8 4 |
5 ≤ Едеф ≤ 8 |
В. В. Казанцев |
|
1 4 |
Суглинки в е рхних террас р. Амур |
То же |
lg E деф = 0,51· 10-6 V 2 p + 2,50 |
0,83 |
5 ≤ Едеф ≤ 76 |
В. В. К аз анце в |
|
|
НЕСВЯЗНЫЕ И СВЯЗН Ы Е ГРУНТЫ |
|
|
|
|
|
|
1 5 |
Песча н о-глини сты е грун ты н еводон асы щенные |
Ур а л, Западная Сибирь |
E деф = 0 ,1076 E д - 1,9 |
0 ,9 0 |
5 ≤ Едеф ≤ 37 |
В. И. Бонд арев |
|
1 6 |
То ж е |
-«- |
E деф = 0 ,154 Vs - 12 |
0,85 |
6 ≤ Едеф ≤ 32 |
В. И. Б ондарев |
|
1 7 |
-«- |
-«- |
E деф = 0 ,116 E д - 4,2 |
0,93 |
4,5 ≤ Едеф ≤ 62 |
В. И. Бондарев |
|
1 8 |
Песча но-г лини стые грунты естеств енной влажности |
Ростов ск ая обл. |
E деф = 0 ,064 E д + 3,5 |
0, 91 |
5 ≤ Едеф ≤ 65 |
Е. С. Гри горчу к |
|
19 |
П есчано-г лини стые грун ты |
Юг Укр аины |
|
- |
2 ≤ Едеф ≤ 90 |
B. E . Василевский |
|
20 |
П есчано-г лини стые грун ты неводонасыщенные |
Все районы СССР |
E деф = 0 ,0936 E д + 0,4 |
0,89 |
4,5 ≤ Едеф ≤ 62 |
В. И. Бонда рев |
4.8. Модуль общей деформации Едеф может быть найден с помощью:
простейших корреляционных уравнений связи (табл. 5);
многомерного корреляционного урав н ения для четв ертичных суглинков различных районов СССР;
теоретико-экспериментальных зависимостей для глинистых грунтов различных районов СССР;
теоретико-экспериментальных з ависимостей д ля любых песчано-глинисты х грунтов отдельных регионов СССР.
4.9. Выбор конкретных уравнений связи, содержащихся в табл. 5, выполняют согласно п. 4.4. Наиболее обос н ованными и проверенными на практике являются линейные зависимости модуля общей деформации Едеф от динамического модуля упругости Е g . Все зависимости такого рода сведены вместе на рис. 9. Менее тесная связь Едеф имеет место со скоростью только продольных или поперечных волн.
4.10. Многомерное корреляционное уравнение (данные Ц НИИС) позволяет определять модуль общей деформации (для нагрузок 0,3-0, 4 МПа) на основе скоростей продольных Vp и поперечных волн Vs , а также плотности скелета γ ск и предела текучести W Т :
Едеф = 0,0060 Vp + 0,0732 Vs + 15,94 γ ск + 2,274( W Т - 27,8) (γск - 1,56) - 29,22. (36)
Уравнение характеризуется коэффициентом множественной корреляции R = 0,83. Область применения уравнения лежит в пределах 7 ≤ Едеф ≤ 30 МПа. При неизвестных з начениях γск и W Т их определяют согласно п. 4.15.
4 . 11. Теоретико-экспериментальные зависимости (данные ЦНИИС) получены на основе стандартной реологической модели сплошной среды и откорректированы на экспериментальном материале [ 16]. При определении модуля общей деформации Едеф нужно знать величины скоростей Vp и Vs , а также декрементов поглощения νp и νs продольных и поперечных волн. Расчет производят в следующем порядке.
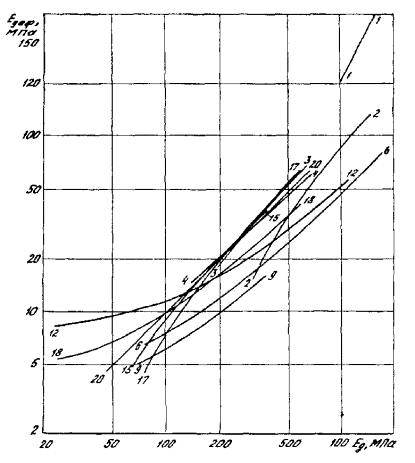
Рис. 9. Графики зависимости модул я общей д еформации Едеф от динамического модуля упругости Е g (номера графиков и характеристики пород см. в табл. 5)
Определяют реологический параметр
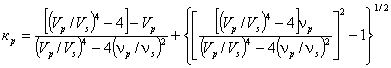 . (37)
. (37)
Рассчитывают теоретический модуль длительной деформации стандартной линейной модели
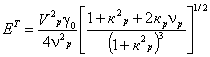 . (38)
. (38)
При кр > 3 рекомендуется пользоваться (с погрешностью менее 10 %) более простым соотношением:
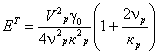 . (39)
. (39)
Переход от теоретического к реальному компрессионному модулю общей линейной деформации Екдеф.л, МПа, т.е. корректировку теоретической зависимости ( 38 ), выполняют по корреляционному соотношению
Екдеф.л = 4,5 + 0,308 ЕТ. (40)
Уравнение характеризуется коэффициентом парной корреляции r = 0,85.
Исходя из общей обоснованности данного подхода и имеющихся э кспериментальных данных, расчет Екдеф.л по формулам ( 38)-( 40) можно производить для любых глинистых грунтов в диапазоне 5 ≤ Екдеф.л ≤ 30 МПа.
Модуль общей деформации Екдеф для требуемой нагрузки σ в области нелинейной зависимости деформации от напряжения определяют по формуле
![]() , (41)
, (41)
где f ( σ ) - функция напр я жения (например, thσ или arcshσ ), подбираемая и з оп ыта [ 24, 25].
Переход от компрессион н ого модуля обще й деформац ии Екдеф и модулю общей деформации Едеф осуществляют по формул е
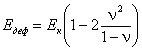 . (42)
. (42)
При отсутствии декремента поглощения поперечных в олн νs Едеф р а ссчитывают в следующем порядке.
Через динамический эффективный модуль Еэф g = V 2 p γ 0 по корреляционной з ависимости определяют Hg , МПа:
Hg = 1,59 Еэф g - 90, (43)
характер из ующейся коэффициентом корреляции r = 0,92. Далее по функциональному уравнению находят параметр к p
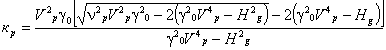 . (44)
. (44)
Теоретический модуль длительной деформации ЕТ определяют по формуле
![]() . (45)
. (45)
или по формулам ( 38) и ( 39).
Дальнейшие расчеты Екдеф и Едеф выполняют по формулам ( 40)-( 42) а н алогично предыдущей схеме.
4.12. Способ расчета с помощью теоретико-экспериментальных зависимостей для любых песчано-глинист ы х грунтов отдельных регионов СССР заключается в том, что, з адаваясь группой физических характеристик грунта, главными из которых являются пористость n , степень влажности g , к оэффициент Пуассона ν и глубина залегания h , можно определить соответствующие им скорость Vp и динамический модуль Eg (задаваясь ν ) по модели дискретной зернистой среды , предложенной В. И. Бондаревым [ 20 ], а модуль общей деформации E деф - по СНиП- II - 1 5-74 (ч. II , гл. 15) [ 26 ] или аналогичным им региональным нормам.
Задаваясь численными значениями этих исходных характеристик в диапазоне их возможного изменения , характерного для интересующего нас типа грунта и условий его залегания, можно рассчитать серию значений E деф и Vp (или Eg ), ограничивающих область взаимосоответствия между анализируемыми характеристиками, и найти (или проверить) соответствующие уравнения взаимосвязи между ними.
Для расчета Vp требуются следующие простейшие физические параметры:
γ0 , γ0Г, γгаз, γж - плотность зерен кварца, глин исты х частиц, газа и жидкости соответственно;
V 0 , V 0Г , V газ , V ж - скорости прод о льных волн в з ернах кварца, глинистой оболочке, газе и жидкости соответственно;
ν 0 , ν Г - коэффициент Пуассона зерен кварца и глинистой об олочки;
к - относительная доля глинистых частиц в скелете грунта (в ядрах);
n , g - пористость и степень влажности грунта соответственно;
h - глубина залегания грунта.
Все параметры кварцевых зерен, газа и жидкости являются постоянными величинами и имеют свои численные значения. Практически постоянным является также плот ность глинистых частиц γ 0Г .
Ввиду малого измен ен ия νГ ему при расчетах присваивается какое-то усредненное численное значение. Величину V Г , м/с, конкрет н ых типов грунтов, что определяе тся чи сленной ве личи ной п араметра К, рекомендуется рассчи тывать по следующим эмпирическим зависимостям [ 20]:
для пес ков (К = 0,020)
![]() ; (46)
; (46)
для супесей (К = 0,065)
![]() ; (47)
; (47)
для суглинков (К = 0,200)
![]() . (48)
. (48)
Численные значения n , g и h задаются в качестве исходных данных.
Примечание . Для точной оценки внутренних сил сцеплени я (давления связности Pc ) требуется знание также величин сцепления С и угла внутреннего трения φ грунта. Однако их зависимость от пористости позво ляет да ть для конкретных типов грунтов эмпирические формулы, обеспечивающие практические расчеты без С и φ .
Скорость продольных волн в среде согласно данной теории опред е ляется по формуле
![]() , ( 49)
, ( 49)
где V об и V к - объемная и контактная составляющие скорости со отве тственно.
Для выражен и я V об и V к в в одятся в сп ом огател ьны е величины:
плотность глин и стой оболочки
γ Г = γ0Г (1 - n ) + gnγ ж ; (50)
относительная доля глинистых частиц в грунте
![]() ; (51)
; (51)
относительная доля кварцевых зерен в ядре (шаре)
n 0 = 1 - n - n 0Г ; (52)
эффективная плотность ядра
![]() ; (53)
; (53)
эффективная плотность грунта
γ э = γ0 n 0 + γ 0Г n 0Г + gnγ ж ; (54)
эффективный коэффициент Пуассона ядра
![]() ; (55)
; (55)
эффективная пористость среды
![]() . (56)
. (56)
Тогда объемную составляющую V об скорости Vp можно выразить соотношен и ем
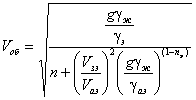 , (57)
, (57)
где V за и V аэ - эффективные скорости в поровом за п ол нителе и ядре соответственно.
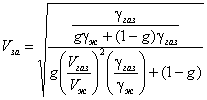 ; (58)
; (58)
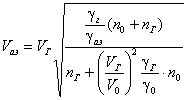 . (59)
. (59)
Соответственно контактная составляющая VK скорости Vp в формуле ( 49) выражается соотношением
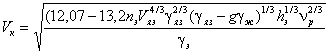 , (60)
, (60)
гд е ![]() ; (61)
; (61)
h э = h + hc - эффективная глубин а. (62)
Глубина связности hc , с м, рассчи тывается с помощью эмпирических формул, составленных на основ е анализа данных СНи П- II - 1 5-74:
для песков
![]() ; (63)
; (63)
для супесей
![]() ; (64)
; (64)
для суглинков
![]() ; (65)
; (65)
Примечан ие . Более т очные расчеты hc для любых г рунтов выполняют по формуле
![]() ; (66)
; (66)
Для практических расчетов Vp на основе данной модели рекомендуются следующие численные значения параметров: γ 0 = 2650 кг/м3; γ 0Г = 2750 кг/м3; γ газ = 1 , 27 кг/м3; γж = 1000 кг/м3; Vp 0 = 6 000 м/с; Vs 0 = 4100 м/с; V газ = 340 м/с; V ж = 1450 м/с; ν0 = 0,1; νГ = 0 , 4. Среднее содержание глинистых частиц: для песков К = 0,020, для супесей К = 0,065 и для суглинков К = 0,200.
Примечан ие . Существуют и другие , в том числе более совершенные, модели, которые в принципе могут быть использованы для расчета сейсмических характеристик по первичным физическим свойствам [ 27, 28]. Однако они трудно реализуемы для практических целей, так как включают параметры, численные з начения которых установить экспериментально довольно сложно.
4.13. Сдвиговые характеристики (постоянную сцепления С и угол внутреннего трения φ ) следует в ы числя ть по простейшим корреляционным зависимостям , приведенным в табл. 6 (см. п. 4.4).
Для постоянной сцепления C наиболее тесная с в язь, обоснованная теоретически и подтвержденная эксперимен тально, наблюдается с динамическим модулем сдвига μ g и со скоростью поперечных волн Vs . Связь C со скоростью продольных волн Vp менее тесная и физ и ческ и менее обоснованная.
Для традиционно трудного параметра φ наиболее тесная связь установлена с декрементом поглощения поперечных волн νs .
Соотношение различных уравнений связи, приводимых в табл. 6, и общий характер взаимосвязей С и φ с динамическим модулем сдвига хорошо видны из рис. 10 и 11.
Примечан ие. Численные значения характеристик С и φ сильно зависят от схемы и вида сдвиговых испытаний [ 29, 30] . Однако для большинства корреляционных зав исимостей, кроме зависимостей Ц НИИС, э тот фактор не нашел отражения и, вероятно, не учтен при анализе. Последнее является, возможно, причиной неодинаковых результатов у различных авторов при анализе взаимосвязей для сдвиговых характеристик (в основном φ ).
Определение физических свойств, состояния и состава грунтов
4.14. Общую пористо с ть n и коэффициент пористо ст и e рекомендуется определять двумя способами: с помощью простейших корреляционных зависимостей и по способу В. И. Бондарева.
Та б лица 6
|
Номер формулы и графика |
Типы грунтов |
Районы |
Уравнения связи |
Коэффициенты корреляции |
Пределы применения |
Авторы |
|
|
НЕС ВЯЗНЫЕ И СЛАБОС ВЯЗНЫЕ ГРУНТЫ |
|
|
|
|
|
|
1 |
Пески неводонасыще нны е |
Все районы СССР |
φ = 5,6 4· 10-2μ g + 29 |
0,72 |
30 ≤ φ ≤ 40,5 |
В. Н. Агеев |
|
2 |
-«- |
-«- |
φ = 4,98 · 10-2 Vs + 23,3 |
0,71 |
30 ≤ φ ≤ 40,5 |
В. И. Бондарев |
|
3 |
П е ски водонасыщ енные |
-«- |
φ = 0,378 · 10-4μ2 g + 28,6 |
0, 76 |
28,7 ≤ φ ≤ 38 |
В . И. Б ондарев |
|
4 |
-«- |
-«- |
φ = 8,468 · 10-8V3s + 27,8 |
0,7 1 |
28,7 ≤ φ ≤ 38 |
В. И . Бондаре в |
|
|
НЕСВЯЗНЫЕ И СВЯЗНЫЕ ГР УНТЫ |
|
|
|
|
|
|
5 |
П есчано-г линистые грунты |
Урал , З ападная Сибирь (з ападная часть) |
|
0,88 |
0,040 ≤ С ≤ 0,088 |
В. И . Б ондарев |
|
6 |
-«- |
То же |
|
0,8 0 |
0,010 ≤ С ≤ 0,056 |
В. И. Бондар е в |
|
7 |
-«- |
-«- |
С = 82,37· 1 0-5 μg - 0,01 08 |
0,85 |
0,012 ≤ С ≤ 0,068 |
В. И. Бондарев |
|
8 |
-«- |
-«- |
φ = 45,6 - 7,95 Vp/Vs |
0,92 |
11 ≤ φ ≤ 35 |
В. И. Бондарев |
|
9 |
-«- |
Урал , З ападная Сибирь |
С = 0,0 9 08 - 0,01 68 Vp / Vs |
- |
- |
В . И. Бон даре в |
|
1 0 |
-«- |
То же |
φ = 46,4 - 9,65 Vp / Vs |
0,7 3 |
14 ≤ φ ≤ 35,5 |
В . И . Бондаре в |
|
11 |
П есчан о- глинисты е грунты естественной влажнос ти |
Все районы ССОР |
С = 3,8· 1 0-4 μg + 0,0087 |
0,82 |
0,01 ≤ С ≤ 0,147 |
В . И . Бондаре в |
|
|
СВЯЗНЫЕ ГРУНТЫ |
|
|
|
|
|
|
1 2 |
Лессы и лес со видны е с углинки |
Юг Украины |
С = 4,8· 1 0-4 μg - 0,008 |
0,90 |
0,01 ≤ С ≤ 0,147 |
И . Г. Минд ель |
|
|
|
|
Ускоренный сдвиг |
|
|
|
|
13 |
Четвертичны е суглинки неводонасыщенные |
Средняя полоса Европейской части СССР |
|
0,80 |
0,018 ≤ С ≤ 0,08 |
О. П. Аникин |
|
1 4 |
То же |
То же |
С = 0,000324 Vs - 0,1 7 |
0,76 |
0,018 ≤ С ≤ 0,08 |
О. П. Аникин |
|
1 5 |
-«- |
-«- |
С = 0, 11 7 - 0,051 νp |
0,67 |
0,018 ≤ С ≤ 0,08 |
О. П. Аникин |
|
1 6 |
-«- |
-«- |
φ = 9,1 νR |
0,75 |
5 ≤ φ ≤ 15 |
О. П. А ни кин |
|
17 |
-«- |
-«- |
φ = 0,8 + 0,89 νp |
0,72 |
5 ≤ φ ≤ 15 |
О. П. Аникин |
|
1 8 |
-«- |
-«- |
φ = 1 6,1 - 0,076 μg |
0,65 |
5 ≤ φ ≤ 15 |
О. П. Аникин |
|
1 9 |
-«- |
-«- |
φ = 1 8,2 - 0,0357 Vs |
0,64 |
5 ≤ φ ≤ 15 |
О. П . Аникин |
|
|
|
|
Замедленн ы й сдв иг |
|
|
|
|
20 |
-«- |
-«- |
|
0,82 |
0,005 ≤ С ≤ 0,03 |
О. П. Аникин |
|
21 |
-«- |
-«- |
С = 0 ,0 001 25 V s - 0,0 11 |
0,78 |
0,005 ≤ С ≤ 0,03 |
О. П. Аникин |
|
22 |
-«- |
-«- |
φ = 32 ,5 - 0,099 μg |
0,72 |
15 ≤ φ ≤ 30 |
О. П. Аникин |
|
23 |
-«- |
-«- |
φ = 39,8 - 0,078 Vs |
0,67 |
15 ≤ φ ≤ 30 |
О. П. Аникин |
Таблица 7
|
Номер формулы и графика |
Типы грунтов |
Районы |
Уравнения связи |
Коэффициенты корреляции |
Пределы применения |
Авторы |
|
|
Н ЕСВЯЗНЫ Е И СЛА БО СВЯЗНЫ Е ГРУНТЫ |
|
|
|
|
|
|
1 |
Пески н евод онасыщ енные |
Все районы СССР |
|
0,48 |
0,282 ≤ n ≤ 0,41 5 |
В. И. Б ондарев |
|
2 |
Пески любой степени влаж ности |
-«- |
|
0,63 |
0,282 ≤ n ≤ 0,434 |
В. И. Бондарев |
|
3 |
Пески неводонасыщенные |
-«- |
n = 15,585 / Е g + 0,276 |
0,78 |
0,280 ≤ n ≤ 0,41 5 |
В. Н. Агеев, В. И. Б ондарев |
|
4 |
-«- |
-«- |
e = 37,5 / Е g + 0,364 |
0,80 |
0,391 ≤ е ≤ 0,71 0 |
В. Н. Агеев, В. И. Б ондарев |
|
|
НЕС В ЯЗНЫ Е И СВЯЗНЫ Е ГРУНТЫ |
|
|
|
|
|
|
5 |
Песчано- глин истые грунты неводонасыщ енны е |
Все районы СССР |
|
0,76 |
0,10 ≤ n ≤ 0,35 |
В. И. Б ондарев |
|
6 |
Те же лю бой степени влажности |
-«- |
|
0,76 |
0,10 ≤ n ≤ 0,35 |
В. И. Бондарев |
|
7 |
Те же водон асы щенны е |
-«- |
|
0,65 |
0,10 ≤ n ≤ 0,45 |
В. И. Б ондарев |
|
8 |
П есчан о- глини сты е грунты |
Урал |
е = 1,1 45 - 1,7 64·10-3Е g |
0,84 |
0,451 ≤ e ≤ 1,05 |
В. И. Бондарев |
|
9 |
Элювиально-делювиальные грунты |
Средне-Амурская впадина |
n = 0, 54 - 7,27·10-8 V2 p |
0,83 |
- |
В . В. К азанцев |
|
1 0 |
Аллю виал ьно-о зерные грунты высоких террас |
-«- |
n = 0 ,60 - 14,61·10-8 V2p + 2,08·10-14 V4p |
0,84 |
- |
В. В. Казанцев |
|
|
СВЯЗНЫЕ ГРУНТЫ |
|
|
|
|
|
|
11 |
Че твертичные суглинки неводонасыщ енны е |
Ср едняя полоса Европейской части СССР |
n = 0 , 507 - 0,142·10-3Vp |
0,69 |
0,35 ≤ n ≤ 0,48 |
О. П. Аник ин |
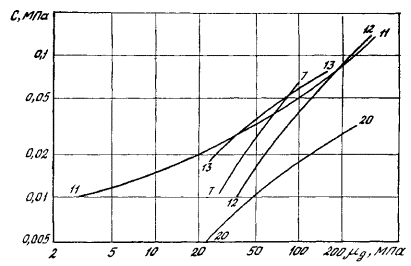
Рис. 10 . Графики зависимости сцепления С от динамического модуля сдвига μ g (номера графиков и характеристики пород см. в табл. 6)
Расчет по первому из них выполняется с помощью корреляционных уравнений , приведенных в табл. 7 (см. п. 4.4). Физически наиболее обоснованной является связь n и e со скоростями продольных Vp и поперечных Vs волн. Соотношение различных ура в нений табл. 7 и общий характер взаимосвязи n с Vp хорошо видны из рис. 12.
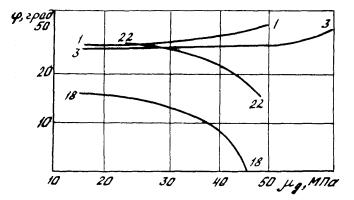
Рис. 11. Графики зависимости угла внутреннего трения φ от динамического модуля сдвига μg (номера графиков и характеристики пород см . в табл. 6)
Расчет n и е по способу В. И. Бондарева аналогичен расчету E деф (с м. п . 4.12). В данном случае отпадает только необходимость в строительных нормах и правилах, так как n является одним из первичных расчетных параметров. Целесообразен анализ взаимосвязи n с Vp .
Примечание . Относительно хорошие результаты при оценке n могут быть получены более простым путем с помощью формулы среднего времени [ 14].
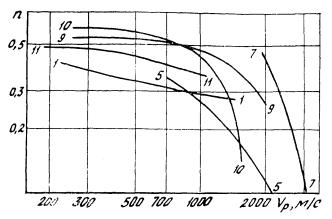
Рис. 12. Гра фи ки з ависимости пористости n от скорости продоль ны х волн V p (номера графиков и характеристики пород см. в табл. 7)
4 .1 5. Плотность γ 0 и пл отн ость скелета γ ск грунта можно опр е делять тремя способами: с помощью простейших корреляци онных уравнений, с помощью множественных корреляц ионных уравнений (данные ЦНИИС) и по модели В. И. Бондарева.
Расчет по первому способу выполняют с помощью уравнений, приведенных в табл. 8 (см. п. 4.4).
Ф и зи чески наиболее обоснованной является связь γ0 и γск со скоростями V p и Vs .
Как показывает практика , взаимосвязь между γ 0 и Vp для рыхлых грунтов различных типов может быть описана степенной функцией вида [ 14]
γ 0 = αVβp , (67)
где α и β - постоянные величины , подлежащие опреде лен ию; для пород суглинистого состава β больше, чем для обломочных грунтов.
Соот н ошен ие различных уравнений табл. 8 и общий характе р в заи мосвяз и γ0 с Vp хорошо видны из р и с. 13.
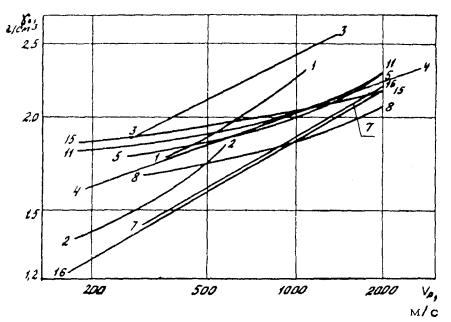
Рис. 13. Графики зависимости плотности γ0 от скорости продольных волн V p (номера графиков и характеристики пород см. в табл. 8)
Табл иц а 8
|
Номер формулы и графика |
Типы грунтов |
Районы |
Уравнения связи |
Коэффициенты корреляции |
Пределы применения |
Авторы |
|
|
НЕСВЯЗНЫ Е И СЛАБОС ВЯЗНЫ Е ГРУНТЫ |
|
|
|
|
|
|
1 |
Галечный ал люв ий с сугли нистым заполнителем |
Северны й Кавказ |
γ 0 = 2 ,23 (10-3 Vp )0,25 |
- |
1 ,73 ≤ γ 0 ≤ 2,30 |
В. Е. Лавров |
|
2 |
Щебень (балласт железнодорожного полотна) |
Все ра й оны ССС Р |
γ 0 = 1,11·10-3 Vp + 1,1 5 |
- |
1 ,35 ≤ γ 0 ≤ 1,8 |
А. М. Б ерман |
|
3 |
Оползневой материал (смесь обломков метаморфических сл а нцев с суглинистым заполнителем) |
Таджикская ССР |
γ 0 = 2 ,43 (10-3 Vp )0,2 |
- |
1 ,85 ≤ γ 0 ≤ 2,6 |
В. Н . Никитин |
|
4 |
Пески любо й степени влажности |
Все районы СССР |
|
0,87 |
1 ,65 ≤ γ 0 ≤ 2,30 |
В. И. Бондарев |
|
5 |
-«- |
-«- |
γ 0 = 0 ,322·10-3 Vp + 1,660 |
0,82 |
1 ,75 ≤ γ 0 ≤ 2,30 |
В. Н. Агеев |
|
6 |
-«- |
-«- |
γ 0 = 0 ,1115·10-2 Vs + 1,410 |
0,8 1 |
1 ,52 ≤ γ 0 ≤ 1,81 |
В. И. Б ондарев |
|
|
СВЯЗНЫЕ ГРУНТЫ |
|
|
|
|
|
|
7 |
Суглинки коры выветриван и я |
Средне-Амурская впадина |
γ0 = 1 ,69 + 0,20·10-6 V2p - 0,02·1012 V4p |
0,77 |
1 ,81 ≤ γ 0 ≤ 2,07 |
В . В. К азанц ев |
|
8 |
Суглин к и верхни х террас р. Амур |
То же |
γ 0 = 1 ,62 + 0,27·10-6 V 2 p - 0,04·10-12 V 4 p |
0,82 |
1 ,73 ≤ γ 0 ≤ 2,07 |
В. В. Казанцев |
|
9 |
Делювиальные суглинки |
Могилев-Подольски й гидроузел |
γ 0 = 1 ,85 (10-3 Vp )0,23 |
- |
- |
В. Н. Никитин |
|
1 0 |
Чет в ертичн ые суглинки неводон асыщ енны е |
Ср е дня я п олоса Европейской части СССР |
γ0 = 1 ,835 + 0,359·10-3 Vp - 0,83·10-3 Vs |
0 , 73 |
1 ,60 ≤ γ 0 ≤ 2,30 |
О. П. Аникин |
|
11 |
То ж е |
То же |
γ 0 = 1 ,719 + 0,29·10-3 Vp |
0 , 67 |
1 ,70 ≤ γ 0 ≤ 2,30 |
О. П. Аникин |
|
1 2 |
Четвертичны е суглинки н еводон асы щенны е |
Средня я полоса Европейской части СССР |
γ ск = 1 ,38 + 0,33·10-3 Vp |
0,67 |
1 ,40 ≤ γ 0 ≤ 2,10 |
О. П . А никин |
|
1 3 |
Лесс ы |
Средняя Ази я |
γ ск = 1 ,19 + 0,475·10-3 Vs |
0,67 |
1 ,40 ≤ γ 0 ≤ 2,10 |
Н. Н . Горяин ов |
|
|
НЕСВЯЗНЫЕ И СВЯЗНЫЕ ГРУНТЫ |
|
|
|
|
|
|
1 4 |
Элювиально-делювиальные грунты |
Урал |
|
0,84 |
1 ,8 ≤ γ 0 ≤ 2,12 |
В . И. Б ондарев |
|
15 |
Песчано-гл ин истые грунты |
-«- |
|
0,77 |
1 ,73 ≤ γ 0 ≤ 2,11 |
В. И. Бондаре в |
|
1 6 |
Песчан о- глини сты е грунты неводо насы щенны е |
Все ра й оны СССР |
γ 0 = 1 ,85 (10-3 Vp )0,232 |
0,7 8 |
1 ,20 ≤ γ 0 ≤ 2,50 |
В. И . Б ондарев |
|
1 7 |
Те ж е любой степени влажности |
|
γ 0 = 2 ,18 (10-3 Vs )0,222 |
0 , 78 |
1 ,20 ≤ γ 0 ≤ 2,50 |
В. И. Бондарев |
Табл ица 9
|
Номер формулы и графика |
Типы грунтов |
Районы |
Уравнения связи |
Коэффициенты корреляции |
Пределы применения |
Авторы |
|
|
|
|
Влажность W , % |
|
|
|
|
1 |
П е ски |
Все районы С С СР |
|
0,78 |
2,4 ≤ W ≤ 23 |
В . И. Б он даре в |
|
2 |
Ч е тве ртичные суглинки |
Средняя полоса Европейской части СССР |
W = 39,88 - 0,01 372 V p - 31,42 Vs/Vp |
0,61 |
9 ≤ W ≤ 30 |
О . П. А ни кин |
|
3 |
Элювиал ь но-делювиальн ые грунты коры выветривания |
Средне-Амурская впадина |
lg W = 3,652 - 0,284 ·10-6 V2 p |
0, 79 |
- |
В. В. Казанцев |
|
4 |
А ллю виально- озерны е г рунты высоких террас |
То же |
lg W = 3,774 - 0,329 ·10-6 V2 p |
0,79 |
- |
В . В. К азанцев |
|
5 |
П е счан о- гли нистые грун ты |
Урал |
W = 38 - 0,031 5 Vp |
0,80 |
9 ≤ W ≤ 30 |
В. И. Бондарев |
|
|
|
|
Степень влаж ности |
|
|
|
|
6 |
Песчаные грунты не водон асыщ енны е |
Вс е рай оны СССР |
g = 0,224 Vp /Vs - 0, 231 |
0,8 6 |
0,1 ≤ g ≤ 0,92 |
В. И. Бондарев |
|
7 |
То же |
-«- |
g = 0,914·10-3 Vp - 0, 209 |
0,9 3 |
0,1 ≤ g ≤ 0,92 |
В . И. Б ондарев |
|
8 |
Пе с чаные грунты люб ой степени влаж ности |
-«- |
g = 0 ,6 62·10-2 Vs - 1 ,022 |
0,85 |
0,10 ≤ g ≤ 1,00 |
В . И. Б ондарев |
|
9 |
Ч е твертичные суглинки неводонасыщенные |
Средняя полоса Европе й ской части СССР |
g = 0,3 09·10-3 Vp + 0,621 |
0,74 |
0,70 ≤ g ≤ 0,98 |
О. П. Аники н |
4. 16 . Согласно второму способу для расчета γ0 и γск че твертичных суглинков всех районов СССР могут быть и спользован ы следующ ие формулы:
γ0 = 2,36 + 0,000103 Vp - 0,563 Vs/Vp - 0,012 WT, (68)
(уравнение характеризуется коэффициентом корреляции R = 0, 88 и справедливо при 1,6 ≤ γ 0 ≤ 2, 30 г/см3);
γ ск = 2,30 + 0,00053 Vs - 0,656 Vs / Vp - 0,0125 W - 0,0121 WT ( 69)
(уравнение характеризуется коэффициентом корреляции R = 0,94 и справедли в о при 1, 40 ≤ γ ск ≤ 2,10).
Для приближенной оценки рекомендуется формул а
γ ск = 2,34 - 0,736 Vs / Vp - 0,0245 W . (70)
Коэффициент корреляции этого уравнения R = 0,91, пределы применения те же, что и для ( 69).
При отсутствии значений W и WT они определяются по значениям Vp и Vs согласно методике, изложенной в п. 4.21, на основе итерационных расчетов.
4.17. Расчет плотности γ 0 и плотности скелета γ ск третьим способом (В. И. Бондарев) аналогичен тому, к ак это сделано для п и Едеф.
4. 18 . Естественную вла жность грунта W можно определять двумя способами: с помощью простейших корреляционных уравнений и с помощью многомерных корреляционных уравнений.
Для расчета по первому способу используют уравнения, приведенные в табл. 9. Из общефизических соо б ражений влажность W наиболее тесно связана с Vp . Наилучший ти п зависи мости указанных величин не установлен, что объясняется сложным поведением скорости Vp в реа л ьных грунтах (особенно связных) при изменении W . Поэтому следует соблюдать особую осторожность при в ы боре расчетного уравнения, а именно: применять только те из них, которые точно соответствуют исследуемому типу грунта, району его распространения и не выходят за указанные пределы применения.
Более высокая надежность определений W для четвертичных суглинков различных районов СССР достигается при использовании множественного корре л яционного уравнения
W = 79,06 - 0,00382 Vp - 30,1 Vs / Vp - 28,91 γ ск . (71)
Уравн е ние хара ктеризуется коэффициентом корреляции R = 0,90 и справ едливо при 9 ≤ W ≤ 30 %.
При отсутствии значений γ ск оно определяется по значениям Vp и Vs согласно методике, и з ложенной в п. 4.21, на основе итерационного процесса.
4.19. Число Wn и верхний предел W Т пластичности н аходят с помощью корреляционных зависимостей (простых и мн огомерных), приведенных в табл. 10 (см. п. 4.4). Нижни й предел пластичности Wp вычисляется как ра з ность Wn - W T .
При отсутствии значений γ 0 и W они определяются по значе ни ям V p и Vs согласно методике, изложенной в п. 4.21, на о снове итерационного процесса.
4.20. Ст е пень влажности g , пока затель консистенции JL и гр ансостав (количество глинистых ГГЛ и п ы леваты х ГПЛ частиц) рассчитывают с помощью простейших корреляцион ных уравнений, приведенных в табл. 9 и 10. Надежность этих расчетов невысока ввиду малой апроби рованности данных зависимостей.
4.21. Наиболее точные и надежные значения влажности W , плотности скелета γ ск (а следовательно, γ0) и верх н его пред ела п ластичности W Т по одним только сейсмическим характеристикам ( Vp и Vs ) могут быть получены на основе итерационного расчета по двум вариа н там.
Первый вариант (сокращенный) предусматривае т расчет W и γ ск (а следовательно , и γ0) по системе из двух многомерных корреляционных уравнений ( 71) и ( 70):
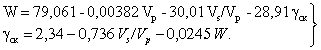 (72)
(72)
Таблица 1 0
|
Номер формулы и графика |
Типы грунтов |
Районы |
Уравнения связи |
Коэффициенты корреляции |
Пределы применения |
Авторы |
|
Числ о плас тичности Wn , %, и предел текучести WT , % |
||||||
|
1 |
Песча н о-г линистые грунты |
Урал |
Wn = 16,4 - 8,73·10-3 Vp |
0,87 |
7 ≤ Wn ≤ 14,8 |
В. И. Бондарев |
|
2 |
Четвертичные суглинки н еводон асыщенные |
Средняя полоса Евр о пей ской части СС СР |
Wn = 0,519 Vs + 0,702 W - 14,6 |
0,76 |
5 ≤ Wn ≤ 17 |
О . П . Аникин |
|
3 |
То ж е |
То же |
WT = 59,92 + 0,660 W - 26,79 γ0 + 0,0078 Vp |
0,84 |
17 ≤ WT ≤ 37 |
О . П . Аникин |
|
4 |
-«- |
-«- |
WT = 26,93 + 0,840 W - 13,143 γ0 + 0,0429 Vs |
0,86 |
17 ≤ WT ≤ 37 |
О . П . Аникин |
|
Показатель консисте н ции |
||||||
|
5 |
П есчано- глини стые грунты |
Ур а л |
JL = 5 6 / μg - 0,83 |
0,93 |
-0,58 ≤ JL ≤ 0,62 |
В . И. Б он дарев |
|
6 |
Четвер т ичные суглинки не водонасы щенны е |
Средняя полоса Европейско й части СССР |
JL = 1,78 - 00791 Vs |
0,78 |
-0,40 ≤ JL ≤ 0,80 |
О. П. Аникин |
|
Г ран сост ав: содержание пылеваты х ГПЛ, % , и глин исты х ГГЛ , % , частиц |
||||||
|
7 |
То же |
Средняя полоса Европе й ской части СССР |
ГПЛ = 96,4 - 0,055 3 Vp |
0,67 |
30 ≤ ГПЛ ≤ 76 |
О. П. Аникин |
|
8 |
-«- |
То же |
ГПЛ = 7,1 + 0,0131 Vp |
0,6 1 |
9 ≤ ГПЛ ≤ 25 |
О. П. Аникин |
В ход в ите рационный процесс производится с помощь ю одноме рн ого уравнения ( 12) таб л. 8.
Второй вариант ( п олный) предусматривает расчет всех упомянутых характеристик по системе из трех многомерных корреляци онных уравнений ( 4) табл. 10, ( 69) и ( 71):
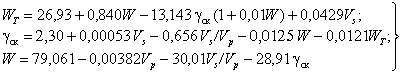 (73)
(73)
Вход в итерационный процесс осуществляется с помощью более простых уравнений ( 12) табл. 9 и ( 2 ) табл. 10.
Для практической реализации итерационного процесса рекомендуется программа "Волна" ( Ц НИИС), которая выполняет оба варианта расчета.
Приложение
(Справочное)
ПРИМЕРЫ ПРАКТИЧЕСКИХ РАСЧЕТОВ
Пример 1. Расчет граничных скоростей и положения преломляющей границы для годографов (см . р ис. 3).
Согла с но
рис. 3 графически с помощью
измерителя строим линии разностного годогра фа θ( x ) и t 0 ( x ) на участке перекрытия встречных годографов ![]() и
и ![]() преломленной волны
(ПК 1 8-52), а также определяем значение t 0 на ПК 0 и ПК 60 по продолжению
годографов (пунктирная линия) . Конфигурация линии t 0 ( x ) с видетельствует о вогнутом характере границы
с увеличением угла наклона на больших ПК.
преломленной волны
(ПК 1 8-52), а также определяем значение t 0 на ПК 0 и ПК 60 по продолжению
годографов (пунктирная линия) . Конфигурация линии t 0 ( x ) с видетельствует о вогнутом характере границы
с увеличением угла наклона на больших ПК.
Определим угол наклона φ границы на наиболее крутой ее части (ПК 35-52) по формуле ( 5)
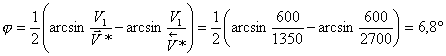 .
.
Ввиду
относительно малого угла наклона границы граничную скорость V Г можно вычислять
по упрощенной формуле ( 6) ,
т.е. по удвоенному коэффициенту угла наклона линии θ( x ): ![]() . Излом разностного годографа θ( x ) в районе ПК 37 свидетельствует об изменении граничной
скорости на профиле в горизонтальном направлении (вертикальный контакт) и
наличии двух участков со скоростями V Г1 = 1950 м/с и V Г2 = 18 00
м/с.
. Излом разностного годографа θ( x ) в районе ПК 37 свидетельствует об изменении граничной
скорости на профиле в горизонтальном направлении (вертикальный контакт) и
наличии двух участков со скоростями V Г1 = 1950 м/с и V Г2 = 18 00
м/с.
По формуле ( 16) рассчитаем глубину границы во всех выбранных точках профиля:
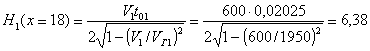 м;
м;
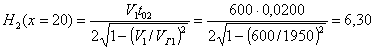 м
м
и т.п.
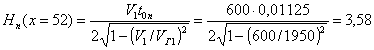 м.
м.
Положение преломляющей границы находим, как огибающую дуг окружностей с центрами на оси x и радиусами r , равными глубине Н в соответствующих точках профиля ( r 1 = H 1 ; r 2 = H 2 , …, rn = Hn ) .
Пример 2. Интерпретация годографов трехслойного разреза при отсутствии участков перекрытия (см. рис. 5).
Определим углы наклона φ 1 и φ 2 для первой и второй преломляющих границ:
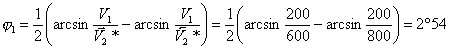 ;
;
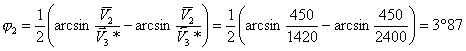 ,
,
где ![]() м/с - средняя скорост ь.
м/с - средняя скорост ь.
Ввиду малости углов φ1 и φ2 наклон преломляющих границ может не учитываться при дальнейших расчетах граничных скоростей и глубин (погрешность менее 1-2 % ).
Найдем значения граничных скоростей V Г1 и V Г2 для первой и второй преломляющих границ:
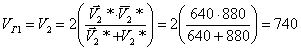 м/с;
м/с;
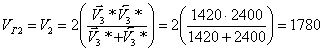 м/с.
м/с.
Рассчиты в аем мощ ности слоев h и глубины залегания границ Н под пунктом возбуждения (ПК 0 и ПК 50).
Способ пласто вых скоростей
Определим крит и ческие углы:
![]() ;
;
![]() ;
;
![]() .
.
Мо щности слоев будут:
![]() м;
м;
![]() м;
м;
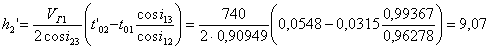 м;
м;
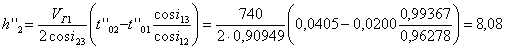 м.
м.
Глубины залегания границ равны:
H ¢ 1 = h ¢ 1 = 3,27 м ; H ¢ ¢ 1 = h ¢ ¢ 1 = 2,08 м ;
H ¢ 2 = h ¢ 1 + h ¢ 2 = 3,27 + 9,07 = 12,34 м ;
H ¢ ¢ 2 = h ¢ ¢ 1 + h ¢ ¢ 2 = 2,08 + 8 , 08 = 10, 16 м .
Величины t 0 найдены путем продолжения ветвей годографов (пунктирная линия) до пересечения с осью времен. Положение второй границы по данным настоя щ их определений нанесено на рис. 5 толстой линией.
Способ средних скоростей
Глубина залегания первой преломляющей границы рассчитывается так же , как при способе пластовых скоростей:
H ¢ 1 = h ¢ 1 = 3,27 м ; H ¢ ¢ 1 = h ¢ ¢ 1 = 2,08 м .
Для второй границы имеем:
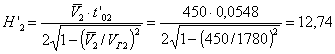 м;
м;
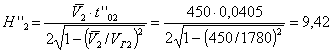 м.
м.
Положение второй границы по данным настоящих определений нанесено на рис. 5 тонкой сплошной линией.
Способ определения глубин по абсциссе точек пересечения годографов
Мощности слоев:
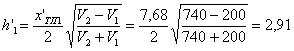 м;
м;
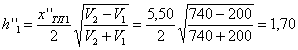 м;
м;
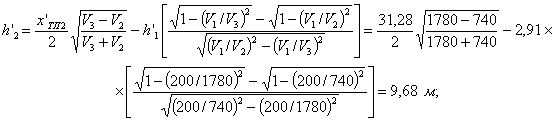
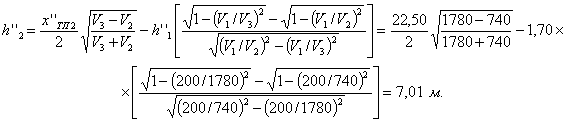
Глубины залегания границ равны:
H ¢ 1 = h ¢ 1 = 2,91 м ; H ¢ ¢ 1 = h ¢ ¢ 1 = 1,70 м ;
H ¢ 2 = h ¢ 1 + h ¢ 2 = 2,91 + 9,68 = 12,59 м ;
H ¢ ¢ 2 = h ¢ ¢ 1 + h ¢ ¢ 2 = 1,70 + 7 , 01 = 8,7 1 м .
СПИСОК ЛИТЕРАТУРЫ
1. Гуревич И . И . Сейсмическая разведк а. М., Недра, 1970.
2. Справочник геофизика, т . IV . «Сейсморазведка». М., Недра, 1966.
3. Гурвич И . И., Боганик Г. Н . Сейсмическая разведка. М ., Недра, 19 80.
4. Методические рекомендации по производ с тву электродинамического зондирования при инженерно-геологических изысканиях. М., ЦНИИС, 1980.
5. Горяинов Н. Н., Ляхови ц кий P . M . Сейсмические методы в инженерной геологии. М., Недра, 1979.
6. Руководство по применению инженерной сейсморазведки при изысканиях для строите л ьства. М., РосглавНИИстройпроект, 1973.
7. Методические рекомендации по применению сейсмоакустических методов для изучения физико-механических свойств связных грунтов. М ., ЦНИИС, 1976.
8. Ляховицкий Ф. М., Парфиянович В . А . Использование ударной установки в производственных сейсмических работах. В сб .: " Раз ведочная геофизика", вы п. 1 . М., Недра, 1964.
9. Рудаков А . Г ., Цы мбал Т. М. О некоторых экспериментальных исследованиях динамических характеристик ударного импульсного воздействия. В сб.: "Вопросы динамической теории распространения сейсмических волн". Л ., Изд-во ЛГУ, 1959.
10. Рекомендации по определению скоростей распространения поперечных волн по данным регистрации поверхностных волн типа Релея и Лява. И МД 75-80. М., Стройизы скания, 1980.
11. Рекомендации по применению вертикального сейсмического профилирования в инженерно-геологических скважинах с целью оценки физико-механических свойств рыхлых грунтов. М ., Стройиздат, 1976.
12. Бондаре в В. И., Писецкий Г. Г., Вербицкий Г. Г. Вертикальное сейсмическое п р офилир ование (ВСП ) инженерно-геологиче ских скважин в строительных целях. - Инженерно-строительные изыс кания, 1976, № 1.
13. Терентьев В . А . Малогабаритный импульсный ультразвуковой сейсмоскоп. М., Изд. АН СССР , сер. "Физика земли", № 11.
14. Ник итин В. Н . Основы инженерной сейсмики. М ., Изд-во МГУ, 1981.
15. Инструкция по применению сейсморазведки в инженерных изысканиях для строительства. РСН 45-77. М ., Госстрой РСФСР, 1977.
16. Рекомендации по определению показателей механических свойств глинистых грунтов по их сейсмоакуст и ческим характеристикам. М., Ц НИИС, 1 984.
17 . Горяинов Н. Н. Сейсмоакустические методы при инженерно-геологических исследованиях рыхлых пород. М., ВСЕГИНГЕО, 1 977.
18 . Кондратьев O . K ., Гамбурцев А. Г. Сейсмические исследования в прибрежной части Восточной Антарктиды. М., Изд-во АН СССР, 1963.
19. Павленкова Н . И., Смелянская Т. В . Методы определения скоростей по годографам преломленных волн. В кн.: "Геофизический сборник" , вып. 2 9. Киев, Наук ова думка, 1969.
20. Бондарев В . И . Сейсмический метод определения важнейших физико-механических характеристик нескальных грунтов. Автореферат на соискание ученой степени д-ра геолого-минералогических наук. Свердловс к , 19 78.
21. Рудницкий В . П . Сейсмические исследования в скважинах (вопросы теории и методики). Киев, Наукова думка, 1968.
22. Савич А . И., Коптев В. И., Никитин В. Н ., Яшенко З. Г . Сейсмоакустические методы изучения массивов скальных пород. М ., Недра, 1 969.
23. Яворский Б. М ., Детлаф А. А . Спра в очник по физике дл я инженеров и студентов в узов. М., Наука, 1964.
24. Месчан С . Р . Ползучесть глинистых грунтов. Ереван , Изд-во АН Армянской ССР, 1967.
25 . Вялов С . С . Реологические основы механики грунтов. М., Высшая школа, 1978.
26. Строительные нормы и правила. Нормы проектирования . Основания зданий и сооружений. СНиП -П-15 -74.
27. Козлов Е. А . О скоростях продольных волн в терригенн ы х отложениях. Известия АН СССР, сер. "Геофизик", № 8, 1962.
28. Назаров Г . Н . Скорости распространения продольных и поперечных волн в грунтовых массивах и основные инженерно-геологические характеристики грунтов. В кн.: "Сейсмическое микрорайонирование ". М., Наука, 1977.
29. Сергеев Е. М . , Голодковская Г. А . и др. Грунтоведение. М ., Изд-во МГУ, 1973.
30. Методическое пособие по инженерно-геологи ч ескому изучению горных пород, т. I - II . М ., Изд-во МГУ, 1968.
СОДЕРЖАНИЕ
|
Предисловие . 1 1. Общие положения . 1 2. Производство работ . 2 Аппаратура и методика наземных сейсмических измерений . 2 Аппаратура и методика наблюдений во внутренних точках среды .. 5 Аппаратура и методика ультразвуковых измерений . 6 3. Обработка и интерпретация материалов сейсмоакустических наблюдений . 6 Обработка и интерпретация материалов наземных наблюдений . 7 Обработка и интерпретация материалов наблюдений во внутренних точках среды .. 13 Обработка и интерпретация материалов ультразвуковых наблюдений . 15 Геологическая интерпретация сейсмоакустических данных . 15 4. Определение физико-механических свойств, состояния и состава нескальных грунтов . 16 Выбор расчетных уравнений . 16 Определение механических свойств грунтов . 17 Определение физических свойств, состояния и состава грунтов . 23 Приложение. Примеры практических расчетов . 32 Список литературы .. 34 |