Измерение как процесс оценивания

Измерение — отображение эмпирической системы в числовую систему, сохраняющую порядок отношений между объектами. Классическая концепция измерения различает два способа приписывания объектам значений переменных. Первый способ называется оцениванием. Отображение свойства объекта на шкалу осуществляется здесь в условных единицах. Например, можно с той или иной степенью точности определить место человека на шкале «консерватизма». Никакой единицы консерватизма в распоряжении исследователя не имеется, градации могут меняться произвольно.

Собственно измерение требует определения единицы —эталона шкалы. В этом случае измерению поддаются лишь пространственные и временные признаки, а также численность — аддитивные величины. Однако в социальных и поведенческих науках получил признание более широкий взгляд на измерение как на приписывание объектам значений в соответствии с заданной системой отношений на различных уровнях.

При анализе измерений следует четко разграничивать два понятия: истинные значения физических величин и их эмпирические проявления — результаты измерений.

Истинные значения физических величин — это значения, идеальным образом отражающие свойства данного объекта как в количественном, так и в качественном отношении. Они не зависят от средств нашего познания и являются абсолютной истиной.

Результаты измерений, напротив, являются продуктами нашего познания. Представляя собой приближенные оценки значений величин, найденные путем измерения, они зависят не только от них, но еще и от метода измерения, от технических средств, с помощью которых проводятся измерения,

и от свойств органов чувств наблюдателя, осуществляющего измерения.

Разница А между результатами измерения X и истинным значением Q измеряемой величины называется погрешностью измерения:

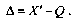
. Но поскольку истинное значение Q измеряемой величины неизвестно, то неизвестны и погрешности измерения, поэтому для получения хотя бы приближенных сведений о них приходится в формулу (11.1) вместо истинного значения подставлять так называемое действительное значение.

Под действительным значением физической величины мы будем понимать ее значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него.

Причинами возникновения погрешностей являются: несовершенство методов измерений, технических средств, применяемых при измерениях, и органов чувств наблюдателя. В отдельную группу следует объединить причины, связанные с влиянием условий проведения измерений. Последние проявляются двояко. С одной стороны, все физические величины, играющие какую-либо роль при проведении измерений, в той или иной степени зависят друг от друга. Поэтому с изменением внешних условий изменяются истинные значения измеряемых величин. С другой стороны, условия проведения измерений влияют и на характеристики средств измерений и физиологические свойства органов чувств наблюдателя и через их посредство становятся источником погрешностей измерения.

Описанные причины возникновения погрешностей определяются совокупностью большого числа факторов, под влиянием которых складывается суммарная погрешность измерения (11.1). Их можно объединить в две основные группы:

•   случайные (в том числе грубые погрешности и промахи), изменяющиеся случайным образом при повторных измерениях одной и той же величины;

•   систематические погрешности, остающиеся постоянными или закономерно изменяющиеся при повторных измерениях.

В процессе измерения оба вида погрешностей проявляются одновременно, и погрешность измерения можно представить в виде суммы:

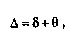
где 8 — случайная, а 6 — систематическая погрешности.

Для получения результатов, минимально отличающихся от истинных значений величин, проводят многократные наблюдения за измеряемой величиной с последующей математической обработкой опытных данных. Поэтому наибольшее значение имеет изучение погрешности как функции номера наблюдения, т.е. времени А(t). Тогда отдельные значения погрешностей можно будет трактовать как набор значений этой функции:

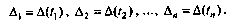
В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времени t. Можно указать лишь вероятности появления ее значений в том или ином интервале. В серии экспериментов, состоящих из ряда многократных наблюдений, мы получаем одну реализацию этой функции. При повторении серии при тех же значениях величин, характеризующих факторы второй группы, неизбежно получаем новую реализацию, отличающуюся от первой.

Реализации отличаются друг от друга из-за влияния факторов первой группы, а факторы второй группы, одинаково проявляющиеся при получении каждой реализации, придают им некоторые общие черты .

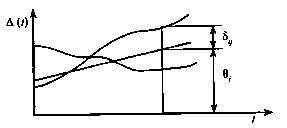
 Рис. Влияние факторов на результаты измерений

Погрешность измерений, соответствующая каждому моменту времени t_p называется сечением случайной функции A(t). В каждом сечении в большинстве случаев можно найти среднее значение погрешности ()i, относительно которого группируются погрешности в различных реализациях. Если через полученные таким образом точки 0i. провести плавную кривую, то она будет характеризовать общую тенденцию изменения погрешности во времени. Нетрудно заметить, что средние значения 0i. определяются действием факторов второй группы и представляют собой систематическую погрешность измерения в момент времени ti, а отклонения лямда ij от среднего в сечении, соответствующие j-й реализации, дают нам значения случайной погрешности. Последние являются уже представителями случайных величин — объектов изучения классической теории вероятностей.

Предположим, что 0(ti) = 0, т.е. систематические погрешности тем или иным способом исключены из результатов наблюдений, и будем рассматривать только случайные погрешности, средние значения которых равны нулю в каждом сечении. Предположим далее, что случайные погрешности в различных сечениях не зависят друг от друга, т.е. знание случайной погрешности в одном сечении как ординаты одной реализации не дает нам никакой дополнительной информации о значении, принимаемом этой реализацией в любом другом сечении. Тогда случайную погрешность можно рассматривать как случайную величину, а ее значения при каждом из многократных наблюдений одной и той же физической величины — как ее эмпирические проявления, т.е. как результаты независимых наблюдений над ней.

В этих условиях случайная погрешность измерений определяется как разность между исправленным результатом Xизмерения и истинным значением Q измеряемой величины:

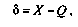
причем исправленным будем называть результат измерений, из которого исключены систематические погрешности.

При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому неясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность.

Функция распределения является самым универсальным способом описания поведения случайных погрешностей.

Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов.

Значительно чаше бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин, называемых моментами.

Наиболее часто применяемыми моментами являются математическое ожидание и дисперсия, поскольку они определяют наиболее важные черты распределения: положение центра распределения и степень его разбросанности. Третий момент случайных погрешностей служит характеристикой асимметрии, или скошенности распределения. В общем случае любой нечетный момент случайной погрешности характеризует асимметрию распределения. Действительно, если распределение обладает свойством симметрии, то все функции вида лямда^sp(8), где s = 1, 3, 5, ..., являются нечетными функциями 5 .

Поэтому все нечетные моменты, являющиеся интегралами этих функций в бесконечных пределах, должны равняться нулю. Отличие этих моментов от нуля как раз и указывает на асимметрию распределения. Простейшим из нечетных моментов является третий момент ц₃[§] • Чтобы получить безразмерную характеристику, третий момент делят на третью степень среднеквадратического отклонения и получают коэффициент асимметрии или просто асимметрию Sk распределения:

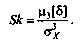
Для иллюстрации сказанного на рис. 11.3 приведены три кривые распределения случайных погрешностей с положительной, отрицательной и нулевой асимметрией.

Четвертый момент служит для характеристики плосковер-шинности или островершинности распределения случайных погрешностей. Эти свойства описываются с помощью эксцесса — безразмерной характеристики, определяемой выражением

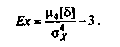
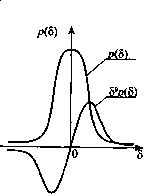
 Рис. Асимметрия распределения

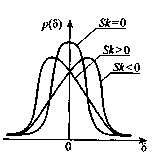
 Рис. Кривые распределения

случайных погрешностей

с положительной, отрицательной

и нулевой асимметрией

Число 3 вычитают из отношения

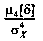
потому, что для

широко распространенного нормального распределения

погрешностей ц₄[8] = 3а⁴_у. Таким образом, для нормального распределения эксцесс равен нулю, более плосковершинные распределения обладают отрицательным эксцессом, более островершинные — положительным .

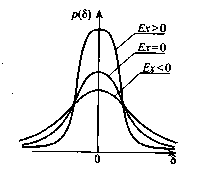
 Рис. Кривые плосковершинности и островершинности распределения случайных погрешностей